Seg Pm is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.
Text Solution
The correct Answer is:QR=16
|
Topper's Solved these Questions
- PYTHAGORS THEORMBook:UNIQUE PUBLICATIONChapter:PYTHAGORS THEORMExercise:HOTS
Explore 1 Video
- PYTHAGORS THEORMBook:UNIQUE PUBLICATIONChapter:PYTHAGORS THEORMExercise:UNIQUE PRACTICE SESSION MCQ.S (3 MARKS QUESTION )
Explore 6 Videos
- PROBABILITY Book:UNIQUE PUBLICATIONChapter:PROBABILITY Exercise:PROBLEM SET 5
Explore 23 Videos
- QUADRATIC EQUATIONS Book:UNIQUE PUBLICATIONChapter:QUADRATIC EQUATIONS Exercise:ASSIGNMENT
Explore 6 Videos
Similar Questions
Knowledge Check
In a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of the aboveIn a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of theseIn ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
AΔDEF≅ΔRPQBΔDEF≅ΔQPRCΔDEF≅ΔQRPDΔDEF≅ΔPQR
In ΔPQR ,seg PM is a median , PM=9 and PQ∘+PR2=290. Find the length of QR.
View SolutionSeg PM is a median of ΔPQR. If PQ=40,PR=42 and PM =29, find QR.
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.
View Solution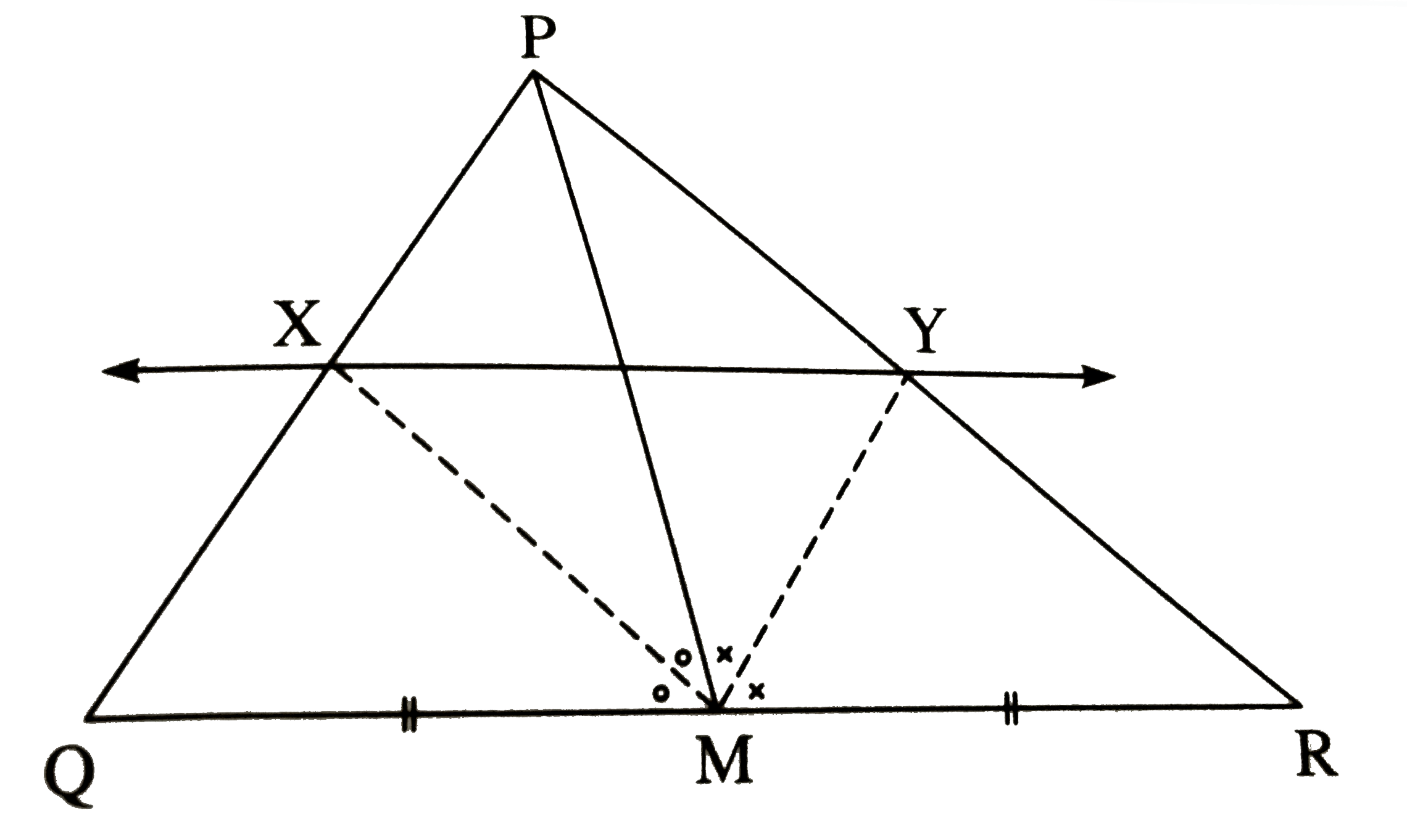
In ΔPQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR interesect side PQ and side PR in points X and Y respectively. Prove that XY∣∣QR.
Complete the proof byfilling in the boxes:
View Solution

