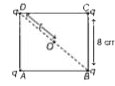
Charges of 103×10−9C are placed at each of the four corners of a square of sides 8cm each. The potential at the intersection of its two diagonals is
900√2V
900V
150√2V
1500√2V
The correct Answer is:D
Given, side length of square 8cm Therefore, the length of the diagonal of square =√(8)2+(8)2=√128=8√2cm
The distance of the intersection of its two diagonals from a charge is
r=8√22=4√2cm
Therefore, potential,
V=4×kqr=4×9×109×103×10−94√2×10−2
∴V=1500√2V
Similar Questions
Knowledge Check
Charges of +103×10−9C are placed at each of the four corners of a square of side 8cm. The potential at the intersection of the diagonals is
A150√2 voltB1500√2 voltC900√2 voltD900 voltA charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
A8Qπε0aB4Q4πε0aC4Q√3πε0aD2Qπε0aFour charges 10−8,−2×108,+3×10−8and2×10−8 coulomb are placed at the four corners of a square of side 1m the potential at the centre of the square is
AzeroB360 voltC180 voltD360√2 volt
Four charges 10−5,−2×10−5,+3×10−5 and 2×10−5 coulomb are placed at the four corners of a square of side 1m the potential at the centre of the square is...
View SolutionFour point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
View SolutionPoint charge of 3×10−9C are situated at each of three corners of a square whose side is 15cm. The magnitude and direction of electric field at the vacant corner of the square is
View SolutionFour charges q1=2×10−8C,q2=−2×10−8C,q3=−3×10−8C and q4=6×10−5C are placed at four corners of a square of side √2m. What is the potential at the centre of the square ?
View SolutionFour charges q1=2×10−8C,q2=−2×10−8C,q3=−3×10−8C and q4=6×10−5C are placed at four corners of a square of side √2m. What is the potential at the centre of the square ?
View Solution
