An electric charge Q is uniformly distributed around a semi-circle of radius a. Calculate the electric potential at the centre of this semi-circle.Solution in Odia
Q is total charge distributed over given semi-circle.
∴ Charge per unit length =QπR
Electric potential at O due to small element PQ is dV and dV= kdq (∵dq=Qπ×dl)
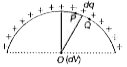
Now, integrate both sides with proper limit, we get
V∫0dV=kQπ2π∫0dl⇒V=kQπ2×π⇒V=kQ
Similar Questions
Draw a semi-circle with centre O and radius 5 cm. Is the diameter that determines the semi-circle, a part of the semi-circle?
View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View SolutionA wire is bent in a circle of radius 10cm. It is given a charge of 250μC which spreads on it uniformly. What is the electric potential at the centre?
View SolutionA metal wire is bent in a circle of radius 20cm. It is given a charge of 400muC which is spread on it uniformly. Calculate the electric potential at its centre.
View SolutionA wire is bent in a circle of radius 10cm. It is given a charge of 250µC which spreads on it uniformly. What is the electric potential at the centre?
View SolutionAn electric charge Q is uniformly distributed around a thin metallic circular coil of single turn and of radius a. Find the expression for the electric potential at a point on its axis at a distance X form its its centre.
View SolutionA metal wire is bent into a circle of radius 10 cm. It is given a charge of 200muC , which spreads on it uniformly. Calculate the electric potential at its centre.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
View Solution
