Three capacitors of capacitances 2μF,4μF and 8μF are joined in series and the combination is connected to a 12 V source. Calculate then energy stored in the combination when these are fully charged. Solution in Odia
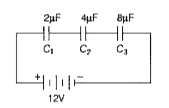
∵C1,C2 and C3 are series combination.
∴1Cs=1C1+1C2+1C3
⇒ 1C8=12+14+18=4+2+18=78⇒C8=87μF
∵ Energy stored in the combination can be given as
E=12C8(V)2=12×87×12×12×10−6
E=8.22×10−5J
Similar Questions
An infinite number of capacitors, having capacitances 1muF, 2muF, 4muF and 8muF….. are connected in series. The equivalent capacitance of the system is
02:17View SolutionA system of 2 capacitors of capacitance 2μF and 4μF is connected in series across potential difference of 6 V. The electric charge and energy stored in the system are
03:31View SolutionAn infinite number of capacitors having capacitances 1muF,2muF,4muF,8muF...... are connected in series. The equivalent capacitance of the system is :
View SolutionTwo capacitors of capacitances C_(1)=2muF and C_(2)=8muF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
04:44View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
01:39View SolutionThree capacitors of capacitances [2muF, 3muF and 4muF] are connected in sereis. : a Find the equivalent capacitance of the combination
02:09View SolutionThree capacitors of capacities 2muF, 4muF and 8muF are joined in series and the combination is connected to a 12V source. Calculate the energy stored in the combination when these are fully charged.
02:39View SolutionThree capacitors of capacitis 4μF,8μFand12μF connected in series. If the charge on the 8μF capacitor is 1201μC then find the charge on each capacitor.
01:24View Solution

