A cell of emf 2V and internal resistance 0.1Ω is connected to a 3.9Ω external resistance. What will be the potential difference across the terminals of cells?
Given, E=2V,r=0.1Ω,R=3,9Ω,V=?
So, potential difference, V=ER+rR
=2×3.93.9+0.1=1.95Ω
Similar Questions
A cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View Solution
Knowledge Check
A cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is
A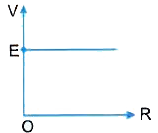 B
B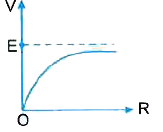 C
C D
D
A cell of emf 2 V and internal resistance 0.1Ω is connected with a resistance of 3.9Ω The voltage across the cell terminal will be
A1.95VB1.90VC0.50VD2.00VA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A(1n)B1(n+1)Cn(n+1)D(n+1)n
A cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
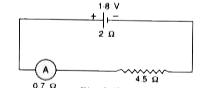
View SolutionA cell of emf ε and internal resistance (r) is connected in series with an external resistance (nr) then the ratio of the terminal potential difference to emf is:
View SolutionA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
View SolutionA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
View SolutionA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
View Solution
