Derive an expression for the magnetic induction at a nearby point of a straight and long current-carrying conductor. Discuss the nature of the magnetic lines of induction.
Text Solution
Consider a straight conductor XY carrying current I. Let us find its magnetic field at a point P at a perpendicular distance a from the point Q of the conductor, i.e. PQ = a
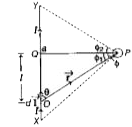
Let a small current element d1 of the conductor at point O. Let the distance of d1 from Q be l, i.e. OQ = l. Let r be the position vector of point P relative to the current element d1 and θ be the angle between d1 and r.
From Biot-Savart.s law, the magnitude of field dB due to current element d1 will be
dB=μ04π⋅Idlsinθr2
From right ΔOQP.
θ+ϕ=90∘⇒θ=90∘−ϕ
∴sinθ=sin(90∘−ϕ)=cosϕ
Also, cosϕ=ar
So, r=acosϕ=asecϕ
As, tanϕ=la
∴l=atanϕ
On differentiating, we get
dl=asec2ϕdϕ
Hence, dB=μ04πI(asec2ϕdϕ)cosϕa2sec2ϕ
dB=μ0I4πacosϕdϕ
The direction of magnetic field due to all such current elements will be normally into the plane of paper.
The total field B due to the entire conductor will be
B=∫ϕ2−ϕ1dB=μ0I4πa∫ϕ2−ϕ1cosϕdϕ
= μ0I4πa[sinϕ]ϕ2−ϕ1=μ0I4πa[sinϕ2−sin(−ϕ1)]
Hence, B=μ0I4πa[sinϕ1+sinϕ2]
|
Similar Questions
Knowledge Check
The magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distanceMagnetic induction at point P from shown current-carrying long conductors is given by-
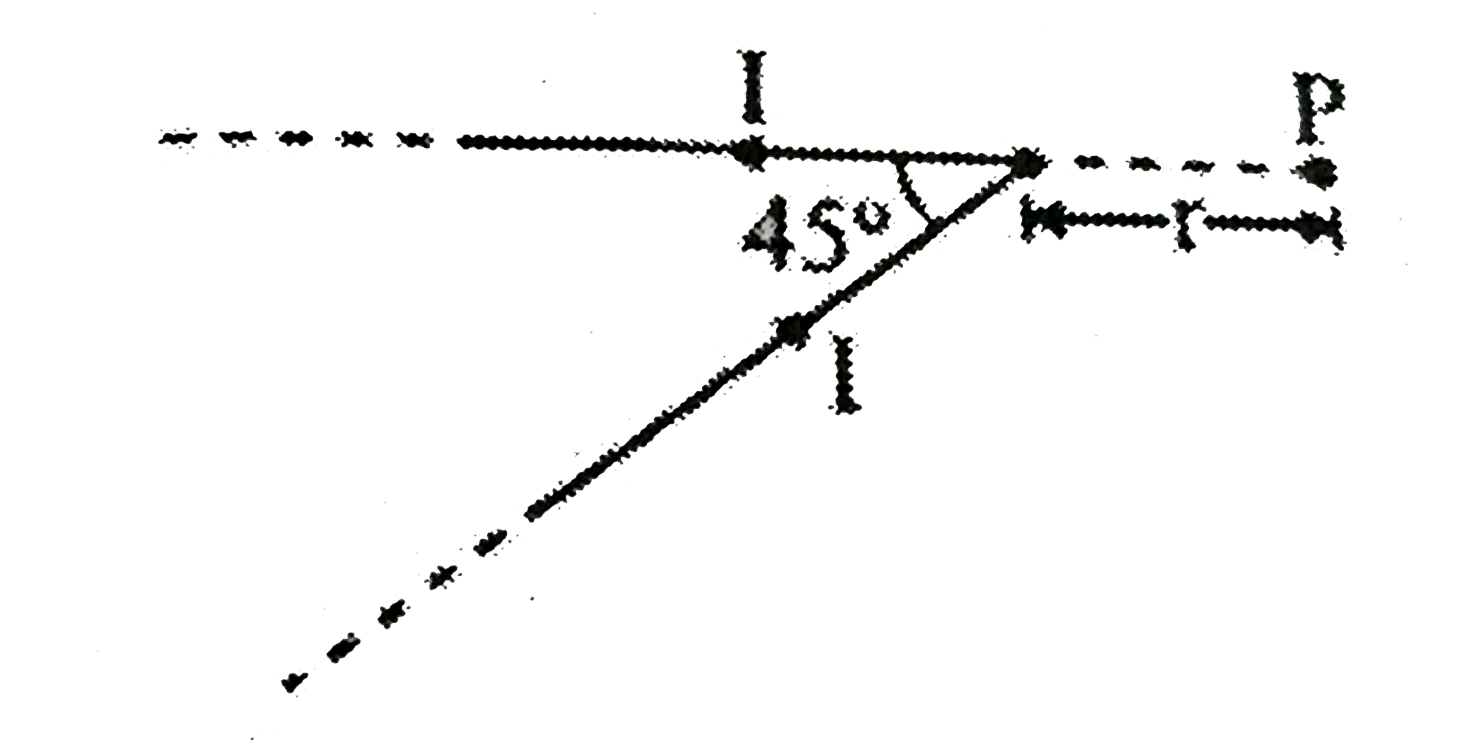 A5μ0I2√2πr(√2−1)Bμ0I√2πr(√2−1)C8μ0I2πr(√2−1)Dμ0I4πr(√2−1)
A5μ0I2√2πr(√2−1)Bμ0I√2πr(√2−1)C8μ0I2πr(√2−1)Dμ0I4πr(√2−1)Magnetic field at a point on the line of current carrying conductor is
AmaximumBinfinityCzeroDfinite value
Write the relation for the magnetic field induction at a point due to a linear conductor carrying current and hence deduce the relation for the magnetic field induction at a point due to a very long linear conductor carrying current.
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
View SolutionThe strength of the magnetic field around a long straight current carrying conductor :
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View Solution
