Deduce an expression for current in an AC circuit containing pure inductance. Show graphically the variation of current and emf with time. Calculate the inductive reactance of an inductor in DC circuit.

Text Solution

Verified by Experts

Suppose in inductor with self - inductance L is connected to an, AC source with instantaneous emf (E ) given by
$E = E_{0} sin ω t$
When key is closed, then current begins to flow because magnetic flux linked it changes and induced emf produces which opposes the applied emf.
According to Lenz.s law,
$e = - L \frac{d I}{d t}$
where , e is induced emf and $\frac{d I}{d t}$ is the rate of change of current.
To maintain the flow of current in the circuit, applied voltage must be equal and opposite to the induced emf.
$E = - e$
$∴ E = - (\frac{- L d I}{d t}) = \frac{L d I}{d t}$
or $d I = \frac{E}{L} d t$
Integrating the above equation on both sides
$\int d I = \int \frac{E}{L} d t$
$I = \int \frac{E_{0} sin ω t}{L} d t [∴ E = E_{0} sin ω t]$
$I = \frac{E_{0}}{L} [\frac{- cos ω t}{ω L} [∴ sin (\frac{π}{2} - ω t) = cos ω t]$
$I = - \frac{E_{0}}{ω L} sin (π / 2 - ω t)$
$I = \frac{E_{0}}{ω L} sin (ω t - π / 2)$
If sin $(ω t - π / 2)$ = maximum = 1, then I = $I_{0}$
where, peak value of current,
$I_{0} = \frac{E_{0}}{ω L}$
$I = I_{0} sin (ω t - π / 2)$
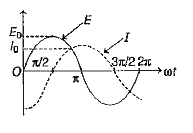
From Eqs. (i) and (iii), it is clear that in a pure inductor, the current lags behind the voltage by a phase angle of $π / 2 (90^{\circ})$ or the voltage leads the current by a phase angle of $90^{\circ} (π / 2)$ .
Graphical representation
The phasor representation of AC ciccuit containg inductor only is given in the figure below:

The figure below shows the phasor diagram of an AC circuit containg capacitor only.

From the graph, it is clear in pure inductance AC circuit, the current lags behind the voltage $π / 2$
For DC, frequency, f = -0
So reactance, $X_{L} = 2 π f L = 0$

Updated on:21/07/2023