An object is placed at a distance x1 from the focus of a concave mirror. Its real image is formed at a distance x2 from the focus. Show that the focal length of the mirror is √x1x2.
Now, according to mirror equation,
1v+1u=1f and
⇒u=f+x1 and v=f+x2
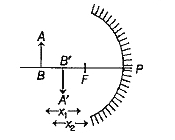
⇒−1(f+x2)−1(f+x1)=1−f
⇒f+x1+f+x2(f+x2)(f+x1)=1f
2f2+fx1+fx2=f2+fx1+fx2+x1x2
⇒f2=x1x2⇒f=√x1x2
Similar Questions
In a concave mirror, an object is placed at a distance d1 from the focus and the real image is formed aat a distance d2 from the focus. Then the focal length of the mirror is :
View SolutionWith a concave mirrorr, an object is placed at a distance x1 from the principal focus, on the principal axis. The image is formed at a distance x2 from the principal focus. The focal length of the mirrorr is
View Solution
Knowledge Check
In a concave mirror, an object is placed at a distance d1 from the focus and the real image is formed aat a distance d2 from the focus. Then the focal length of the mirror is :
A√d1d2Bd1d2C(d1+d2)/2D√d1/d2An object is placed at a distance x1 from the principal focus of a lens and its real image is formed at a distance x2 from the another principal focus. The focal length of the lens is
Ax1x2Bx1x22Cx1+x22D√9x1x2)With a concave mirror, an object is placed at a distance x1 from the principal focus, on the principal axis. The image is formed at a distance x2 from the principal focus. The focal length of the mirror is
Ax1x2Bx1+x22C√x1x2D√x1x2
An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionIn a concave mirror experiment, an object is placed. at a distance x1 from the focus and the image is formed at a distance x2 , from the focus. The focal length of the mirror would be
View SolutionWith a concave mirrorr, an object is placed at a distance x1 from the principal focus, on the principal axis. The image is formed at a distance x2 from the principal focus. The focal length of the mirrorr is
View SolutionIn a concave mirror experiment, an object is placed at a distance x1 from the focus and the image is formed at a distance x2 from the focus. The focal length of the mirror would be
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View Solution
