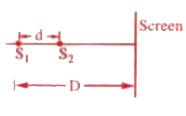
Two coherent source S1andS2 (wavelength =6000Å) are 1.0 mm apart. The screen is placed at a distance of 25 cm from the sources. Calculate the fringe width on the screen.
Given, λ=6000Å=6000×10−10m
Distance between slit and screen, D=25cm=0.25m
and distance between two slits, d=1.0mm=10−3m
Using β=λDd, we get
β=6000×10−10×0.2510−3
=15×10−5m
⇒β=0.015 cm
Similar Questions
Two coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
View SolutionThe distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
View Solution
Knowledge Check
Two coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
A(a) 0.015cmB(b) 0.025cmC(c) 0.010cmD(d) 0.030cmThe distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
A4000ÅB5000ÅC6000ÅD7200ÅIn Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
A25B12C15D20
In Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionA monochromatic point source(S1) is at a distance d from a screen. Another identical source (S2) is at a large distance from the screen. The two sources are on a line which is perpendicular to the screen. Sources are coherent. What is the shape of interference fringes on the screen?
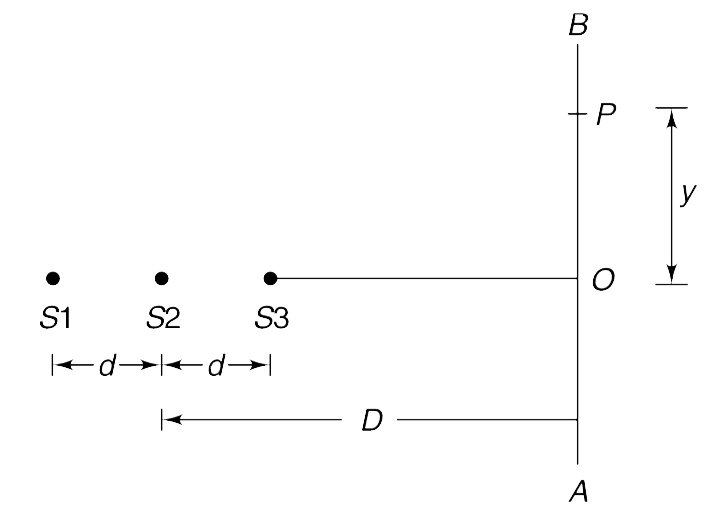
(b) Three identical coherent sources are placed on a straight line with two neighbouring ones separated by a distance d = 0.06 mm. The sources produce monochromatic light of wavelength λ = 550.4 nm. A line AB is located at a distance D = 2.50 m from the sources and is perpendicular to line joining the three sources. Intensity of light at P with any one of the sources switched on is Io. Find the intensity when all three sources are switched on. Distance of point P from O isy = 1.72 cm (see figure)
View SolutionTwo coherent sources are 0.3 mm apart. They are 0.9m away from the screen. The second dark fringe is at a distance of 0.3cm from the centre. Find the distance of fourth bright fringe from the centre. Also, find the wavelength of light used.
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View Solution
