Deduce an expression for the fringe width in Young.s double slit experiment. How does the fringe width depend on the distance between the source and the slits?

Text Solution

Verified by Experts

The experimental arrangement for Young.s double slit experiment is shown in the figure.

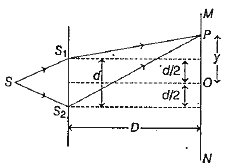
Consider a point P at a distance y from 0, the centre of screen.
The path difference between two waves arriving at P is equal to $S_{2} P - S_{1} P$ .
Now, ${(S_{2} P)}_{2}^{2} - {(S_{1} P)}_{1}^{2}$
$= [D^{2} + {(y + \frac{d}{2})}^{2}] - [D^{2} + {(y - \frac{d}{2})}^{2}] = 2 y d$
Thus, $S_{2} P - S_{1} P = \frac{2 y d}{S_{2} P + S_{1} P}$
But, $S_{2} P + S_{1} P = 2 D$
$∴ S_{2} P - S_{1} P = \frac{d y}{D}$
(i) For constructive interference (Bright fringes, i.e. maxima)
path difference $= \frac{d y}{D} = n λ$ , where $n = 0, 1, 2, 3, ...$
$∴ y = \frac{n D λ}{d} (∵ n = 0, 1, 2, 3, ...)$
Hence, for $n = 0, y_{0} = 0$ at $O$ central bright fringe.
For $n = 1, y_{1} = \frac{D λ}{d}$ for 1st bright fringe
For $n = 2, y_{2} = \frac{2 D λ}{d}$ for $2 n d$ bright fringe
For $n = n, y_{n} = \frac{n D λ}{d}$ for $n t h$ bright fringe
The separation between. two consecutive bright fringes is
$β = \frac{n D λ}{d} - \frac{(n - 1) D λ}{d} = \frac{D λ}{d} \Rightarrow β = \frac{D λ}{d}$
(ii) For destructive interference (dark fringes, i.e. minima)
Path difference $= \frac{d y}{D} = (2 a - 1) \frac{λ}{2}$
or $n = 1, y_{1} = \frac{D λ}{2 d}$ for 1st dark fringe
For $n = 2, y_{2} = \frac{3 D λ}{2 d}$ for 2nd dark fringe
for $n = n, y_{n} = (2 n - 1) \frac{D λ}{2 d}$ for nth dark fringe.
The separation between two consecutive dark fringes is
$β . = (2 n - 1) \frac{D λ}{2 d} - {2 (n - 1) - 1} \frac{D λ}{2 d} = \frac{D λ}{d} \Rightarrow β . = \frac{D λ}{d}$
Thus, all bright and dark fringes are of equal width. From the above relation, fringe width $(β)$ is directly proportional to the distance between the source and the slits (D)

Updated on:21/07/2023

The fringe width in Young’s double slit experiment increases when
AWavelength increases
BDistance between the slits increases
CDistance between the source and screen decreases
DThe width of the slits increases
In the Young’s double slit experiment, for which colour the fringe width is least
ARed
BGreen
CBlue
DYellow
If the frequency of the source is doubled in Young's double slit experiment, then fringe width $(β)$ will be –
Aunchanged
B $β / 2$
C $2 β$
D $3 β$