Define electric filed and electric potential at a point . Derive the expression for the electric field due to an electric dipole at an equatorial point.

Text Solution

Verified by Experts

Electric Field The region surrounding a charge or distribution of charge in which its electrical effects can be observed or experienced is called the electric field of the charge or distribution of charge. Electrostatic Potential The electric potential at any point in the region of electric field is defined as the amount of work done in bringing a unit positive test charge (without acceleration) from infinity to that point along any arbitrary. path.
Electrostatic potential (V) = Work done (w) / Charge $(q_{0})$
Electric field intensity due to an electric dipole at an equatorial point Consider an electric dipole consisting of two point charges + q and -q separated by a small distance AB = 2l with centre at O and dipole moment, p= q(2l) as . shown in the figure:

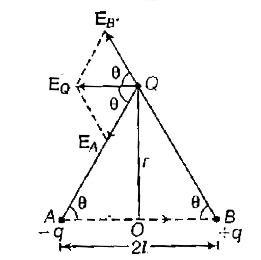
Resultant electric field intensity at the point,Q,
$E_{Q} = E_{A} + E_{B}$
The vectors $E_{A}$ and $E_{B}$ are acting at an angle $2 θ$ .
Here, $E_{A} = \frac{1}{4 π ε_{0}} \frac{q}{(r^{2} + l^{2})}$
$E_{B} = \frac{1}{4 π ε_{0}} \frac{q}{(r^{2} + l^{2})}$
On resolving $E_{A}$ and $E_{B}$ into two rectangular components, the vectors $E_{A} sin θ$ and $E_{B} sin θ$ are equal in magnitude and . opposite to each other and hence cancel out. The vectors $E_{A} cos θ$ and $E_{B} cos θ$ are acting along the same direction and hence add up.
$∴ E_{Q} = E_{A} cos θ + E_{B} cos θ$
$= 2 E_{A} cos θ$
$= \frac{2}{4 π ε_{0}} \frac{q}{(r^{2} + l^{2})} . \frac{l}{{(r^{2} + l^{2})}^{1 / 2}} (∵ cos θ = \frac{l}{{(r^{2} + l^{2})}^{1 / 2}})$
$= \frac{1}{4 π ε_{0}} . \frac{2 q l}{{(r^{2} + l^{2})}^{3 / 2}}$
But q x 2l = |p| , the dipole moment,
$E_{Q} = \frac{1}{4 π ε_{0}} . \frac{| p |}{{(r^{2} + l^{2})}^{3 / 2}}$
The direction of $E_{Q}$ is along QE || BA, i.e. opposite to AB. In vector form, we can rewrite as
$E_{Q} = \frac{- p}{4 π ε_{0} {(r^{2} + l^{2})}^{3 / 2}}$
Obviously, $E_{Q}$ is in a direction opposite to the direction of p. If the dipole is short, i.e. 2l << r, then
$E_{Q} = \frac{1}{4 π ε_{0}} . \frac{| p |}{r^{3}}$

Updated on:21/07/2023

The electrostatic potnetial due to an electric dipole at an equatorial point is
Amaximum
Bzero
Cminimum
Dnot defined
The electric potential at a point on the equatorial line of a electric dipole is
Adirectly proportional to the square of the distance
Bindirectly proportional to the square of the distance
Cdirectly proportional to the charge
Dnone of the above