Define resistance. Derive an expression for net resistance, when resistors are connected in
parallel

Text Solution

Verified by Experts

Resistance in Parallel

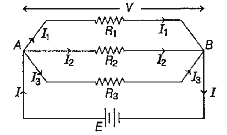
Consider three resistances $R_{1}, R_{2} and R_{3}$ are connected in parallel. Let V be the potential difference applied across A and B using the battery (E) and the main current (I) in the circuit from battery. If $I_{1}, I_{2} and I_{3}$ are currents through the three resistances $R_{1}, R_{2} and R_{3}$ , respectively.
We know that the current is given by
$I = I_{1} + I_{2} + I_{3} ... . (i)$
But potential difference (V) across each resistor is given by
$V = I_{1} R_{1} = I_{2} R_{2} = I_{3} R_{3}$
or $I_{1} = \frac{V}{R_{1}}, I_{2} = \frac{V}{R_{2}}, I_{3} = \frac{V}{R_{3}}$
Substituting $I_{1}, I_{2} and I_{3}$ in Eq. (i), we get
$I = \frac{V}{R_{1}} + \frac{V}{R_{2}} + \frac{V}{R_{3}}$

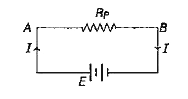
If $R_{P}$ is the equivalent resistance of the given parallel combination of resistances.
Then, $V = I R_{P}$
$∴ I = \frac{V}{R_{P}}$
$\Rightarrow \frac{V}{R_{P}} = \frac{V}{R_{1}} + \frac{V}{R_{2}} + \frac{V}{R_{3}} \Rightarrow \frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}$

Updated on:21/07/2023

Equivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
A $R_{p} = \frac{R_{1} + R_{2}}{R_{1} R_{2}}$
B $R_{p} = \frac{R_{1} R_{2}}{R_{1} - R_{2}}$
C $R_{p} = \frac{R_{1} - R_{2}}{R_{1} + R_{2}}$
D $R_{p} = \frac{R_{1} + R_{2}}{R_{1} + R_{2}}$
R is the equivalent resistance of n resistors of same resistance in series. If the connection is turned parallel then equivalent resistance will be:
A $n^{2} R$
BnR
C $\frac{R}{n}$
D $\frac{R}{n^{2}}$
The equivalent resistance of n identical resistors connected in parallel is x. If the resistors are connected in series, the equivalent resistance would be
An x
B $n^{2} x$
Cx/n
D $x / n^{2}$