There are two charged conducting sphere of radii r1andr2 .Find the (i) ratio of the charge on them if both of them are at the same potential (ii) ratio of potential if the charge on them are equal .
(i) Here , V = constant and Q = CV
So , Q∝C
⇒Q1Q2=C1C2=4ε0r14ε0r2=r1r2
(ii) Here , Q = constant and V = QC
So , V∝1C⇒V1V2=C2C1=r2r1
Similar Questions
Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is
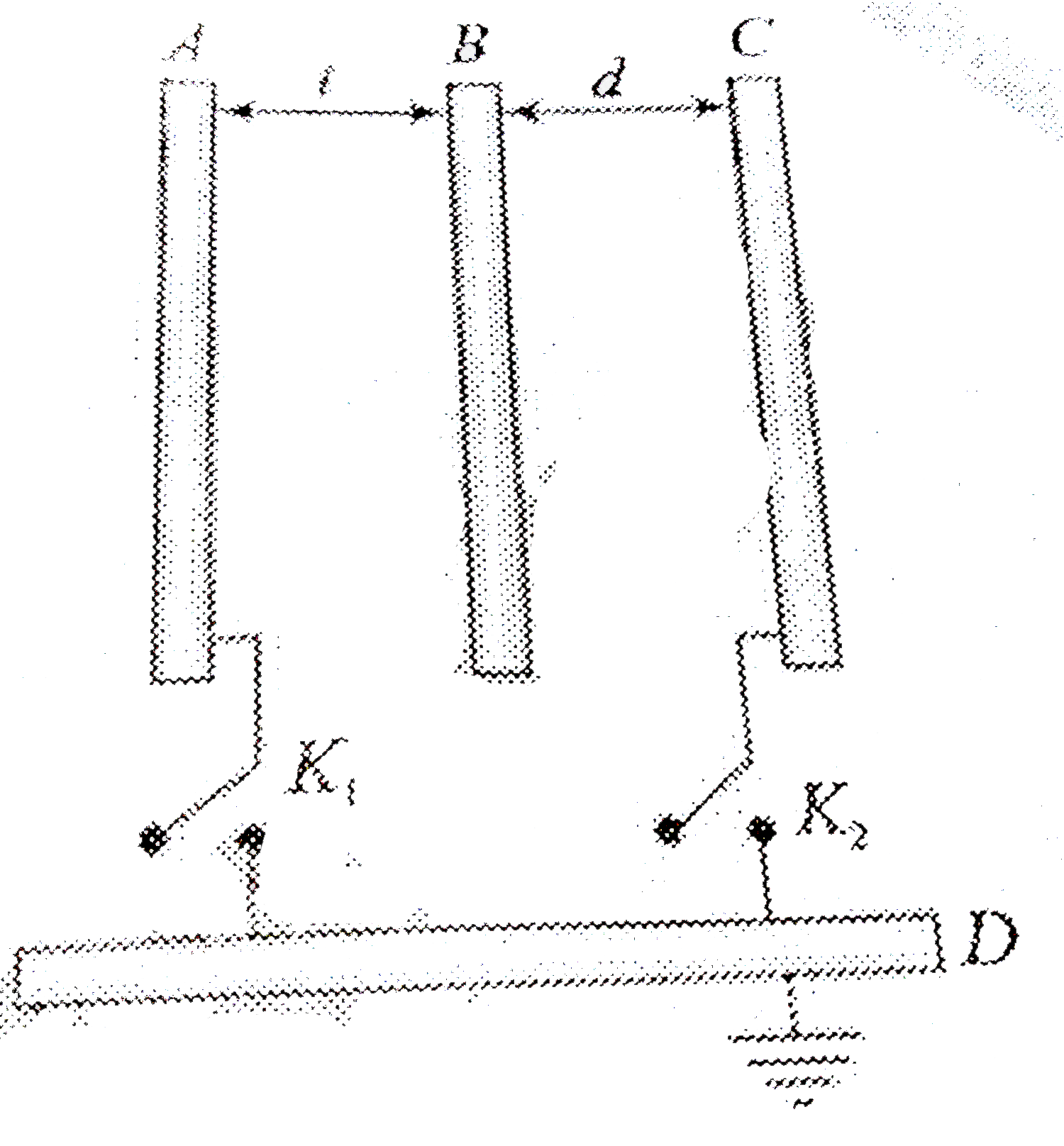
View Solution
Knowledge Check
Two conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
Ar21/r22Br22/r21Cr1/r2Dr2/r1Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
AR1/R2BR2/R1C(R1/R2)2D(R2/R1)2Two conducting spheres of radii r1 and r2 are charged to the same surface charge density . The ratio of electric field near their surface is
Ar21/r22Br22/r21Cr1/r2D1:1
A charge Q has been divided on two concentirc conducting spheres of radii R1andR2(R1>R2) such that the surface charge densities on both the sphere is same. Find the potential at their common center.
View SolutionA charge Q has been divided on two concentirc conducting spheres of radii R1andR2(R1>R2) such that the surface charge
densities on both the sphere is same.
Find the potential at their common center.
View SolutionConsider two conducting spheres of radii R1andR2 with R1>R2. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whetehr the charge density of the smaller sphere is more or less than that of the larger oe.
View SolutionTwo metal spheres of radii R1 and R2 are charged to the same potential. The ratio of charges on the spheres is
View SolutionA charge Q has been divided on two concentric conducting spheres of radii R1 and R2(R1>R1) such that the surface charge densities on both the spheres are equal. The potential at their common centre is
View Solution
