An archery target has three regions formed by three concentric circles as shown in the given figure. If the diameters of the circle are in ratio 1:2:3, then find the ratio of the areas of three regions.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:1:3:5
Step by step video, text & image solution for An archery target has three regions formed by three concentric circles as shown in the given figure. If the diameters of the circle are in ratio 1:2:3, then find the ratio of the areas of three regions. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.15videos
AREAS RELATED TO CIRCLES
- BOOK - KUMAR PRAKASHANCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.214videos
AREAS RELATED TO CIRCLES
- BOOK - KUMAR PRAKASHANCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Objective Questions25videos
AREAS RELATED TO CIRCLES
- BOOK - KUMAR PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - OBJECTIVE QUESTIONS1videos
ARITHMETIC PROGRESSION
Similar Questions
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumference of the two circles.
04:22View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60∘.
04:22View SolutionFill in the blanks so as to make each of the following statements true :
The difference between the circumference and radius of a circle is 37 cm. Then the circumference of the circle is………03:53View SolutionAnswer each question by selecting the proper alternative from those given below each question so as to make each statement true :
If the common difference of an AP is 5. then value of ,a18−a13 is .....02:45View Solutionfind of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. then find the ratio of the areas of three regions Fig.15.8
02:17View Solutionfind of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. then find the ratio of the areas of three regions Fig.15.8
05:41View SolutionFind the area of the shaded region, given that the radius of each circle is equal to 5 cm.
03:28View SolutionMatch the following Column A to Column B
 02:21View Solution
02:21View SolutionMatch the following Column A to Column B
 02:03View Solution
02:03View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionFind the area of figure given below.
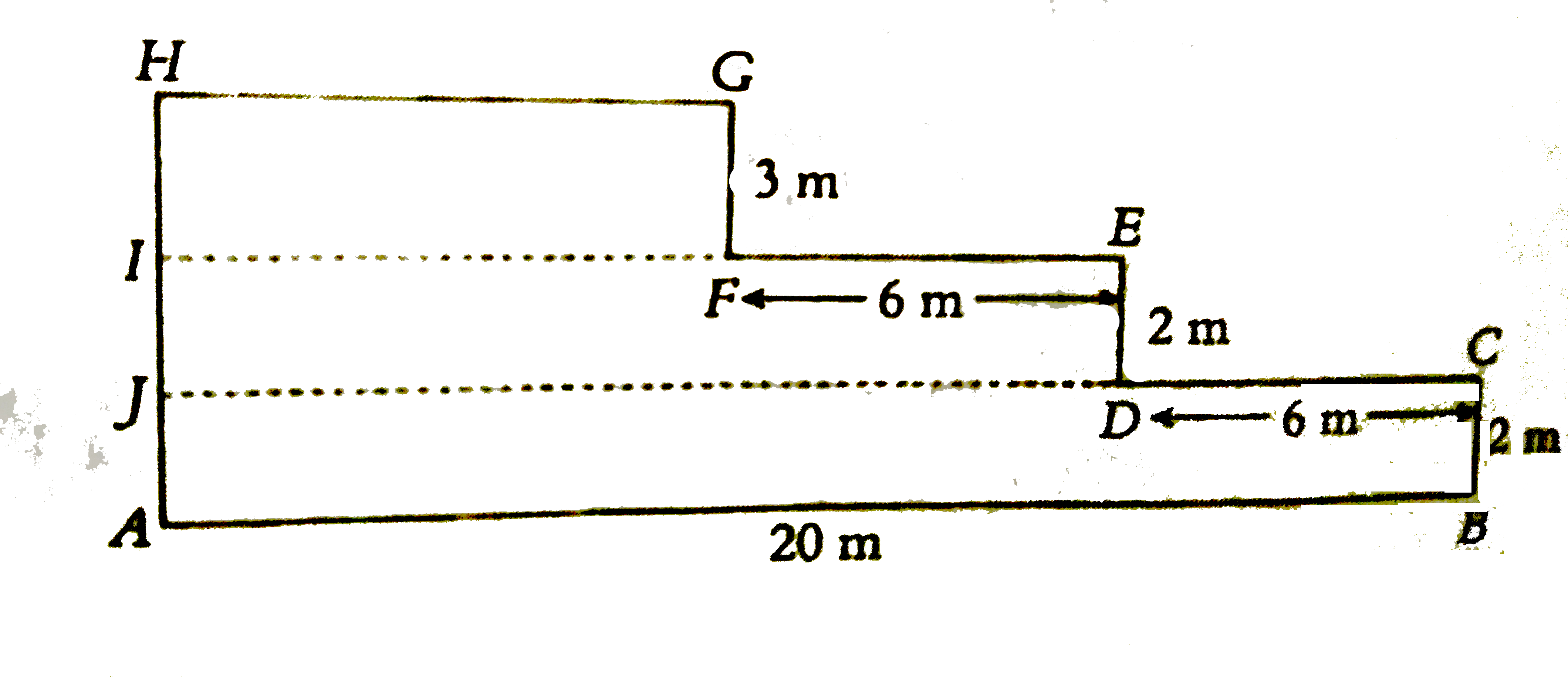 02:17View Solution
02:17View SolutionFind the area of the figure given below.
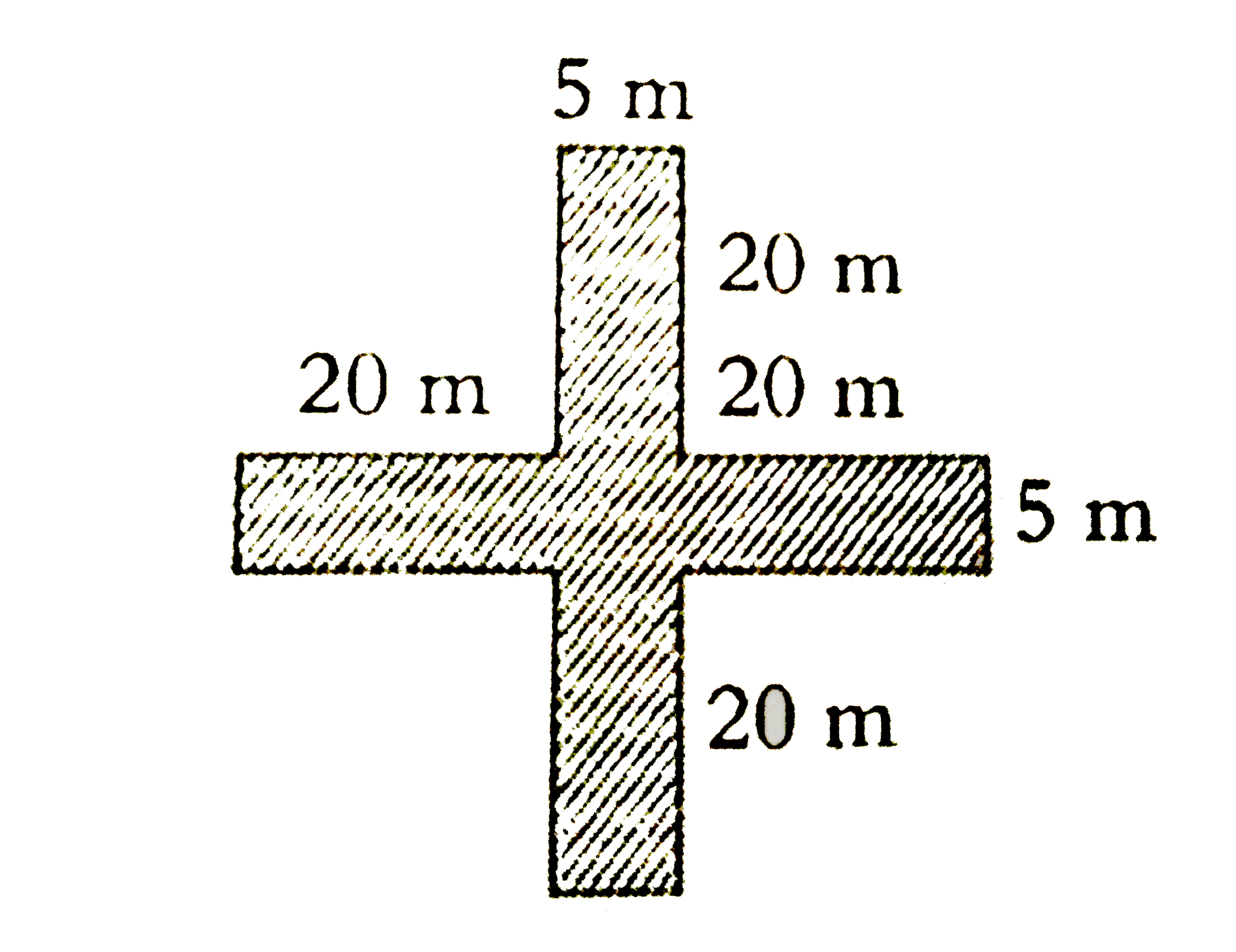 04:23View Solution
04:23View SolutionThe area of the shaded part in the figure given below is ______.
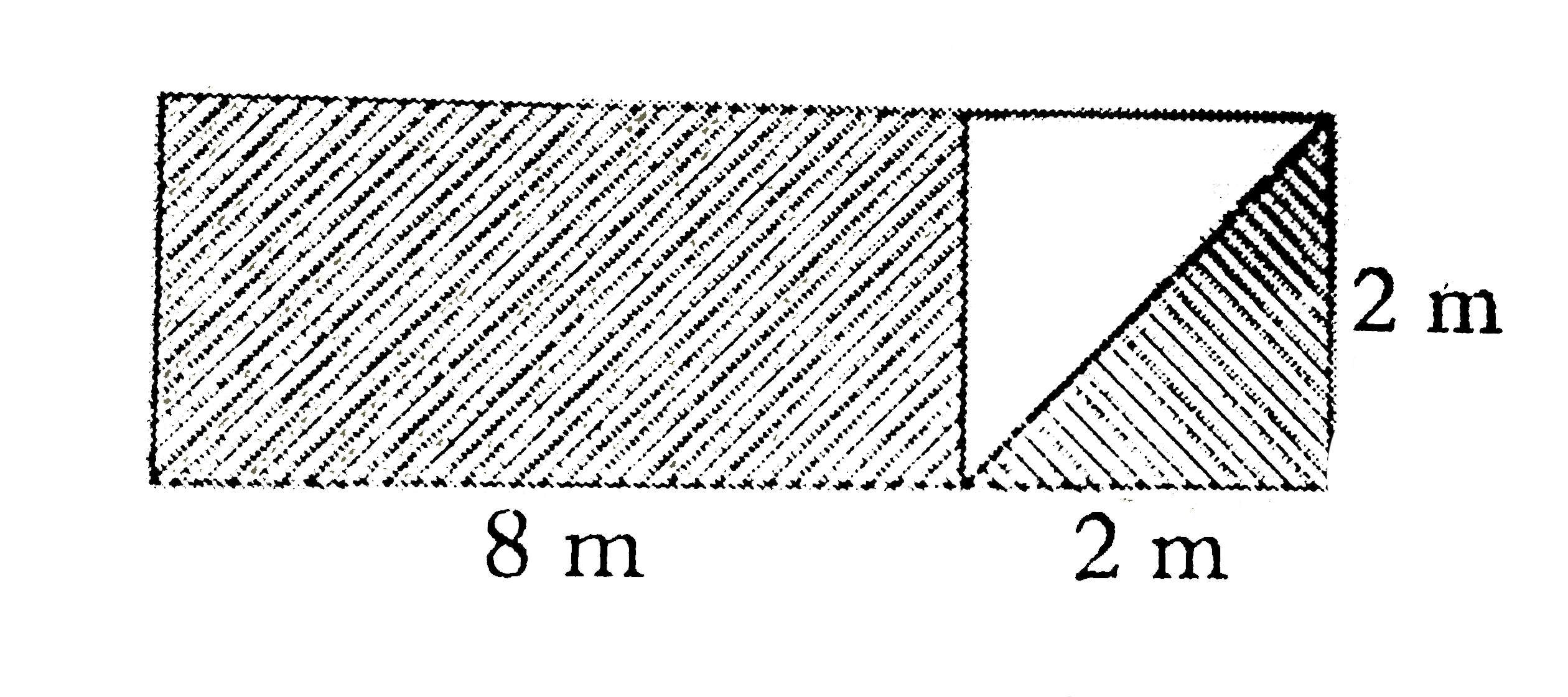 02:02View Solution
02:02View SolutionThe inequation represented by the graph given below is :
03:32View SolutionThe inequation that best describes the graph given below is _________
03:29View SolutionWhich inequations represent the shaded region in the given figure
03:43View Solution

