The area of an equilateral triangle ABC is 17320.5cm2. With each vertex of the triangle as centre, a circle is drawn with radius to half the length of the side of the triangle (see the given figure). Find the area of the shaded region. (Use π=3.14 and √3=1.73205)
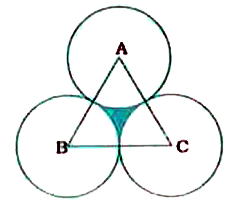 Solution in Gujrati
Solution in Gujrati
The correct Answer is:1620.5cm2
Step by step video, text & image solution for The area of an equilateral triangle ABC is 17320.5 cm^(2). With each vertex of the triangle as centre, a circle is drawn with radius to half the length of the side of the triangle (see the given figure). Find the area of the shaded region. (Use pi = 3.14 and sqrt(3) = 1.73205) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Test Your Skills15videos
AREAS RELATED TO CIRCLES
- BOOK - KUMAR PRAKASHANCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Practice Thoroughly8videos
AREAS RELATED TO CIRCLES
- BOOK - KUMAR PRAKASHANCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.214videos
AREAS RELATED TO CIRCLES
- BOOK - KUMAR PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - OBJECTIVE QUESTIONS1videos
ARITHMETIC PROGRESSION
Similar Questions
The circumference of a circle exceeds its diameter by 30 cm. Find the circumference of the circle.
05:34View SolutionA playground has the shape of a rectangle, with two semicircles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground.
03:53View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60∘.
02:03View SolutionAnswer each question by selecting the proper alternative from those given below each question so as to make each statement true :
If the common difference of an AP is 5. then value of ,a18−a13 is .....04:23View SolutionThe area of an equilateral ΔABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see the figure). Find the area of the shaded region. [Take π = 3.14 and √3 = 1.73205]
01:57View SolutionFind the area of the shaded region, given that the radius of each circle is equal to 5 cm.
05:09View SolutionThe area of the shaded part in the figure given below is ______.
 03:56View Solution
03:56View SolutionWhich inequations represent the shaded region in the given figure
03:43View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View Solutionएक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm2 है। इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
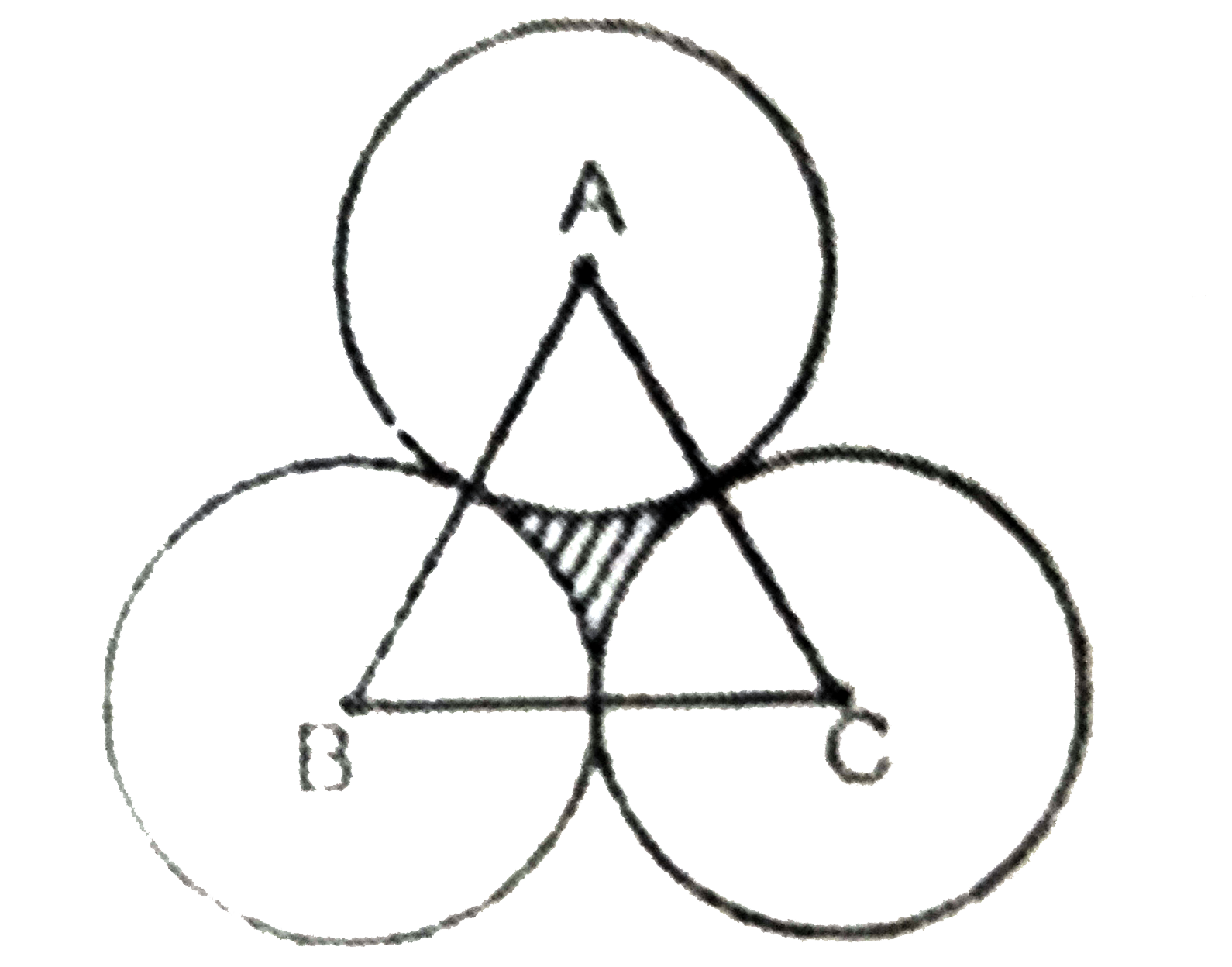 05:04View Solution
05:04View Solutionचित्र में, 6 सेमी. भुजा वाला एक समबाहु त्रिभुज ABC एक वृत्त के अन्दर बनाया गया है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | (π=3.14)
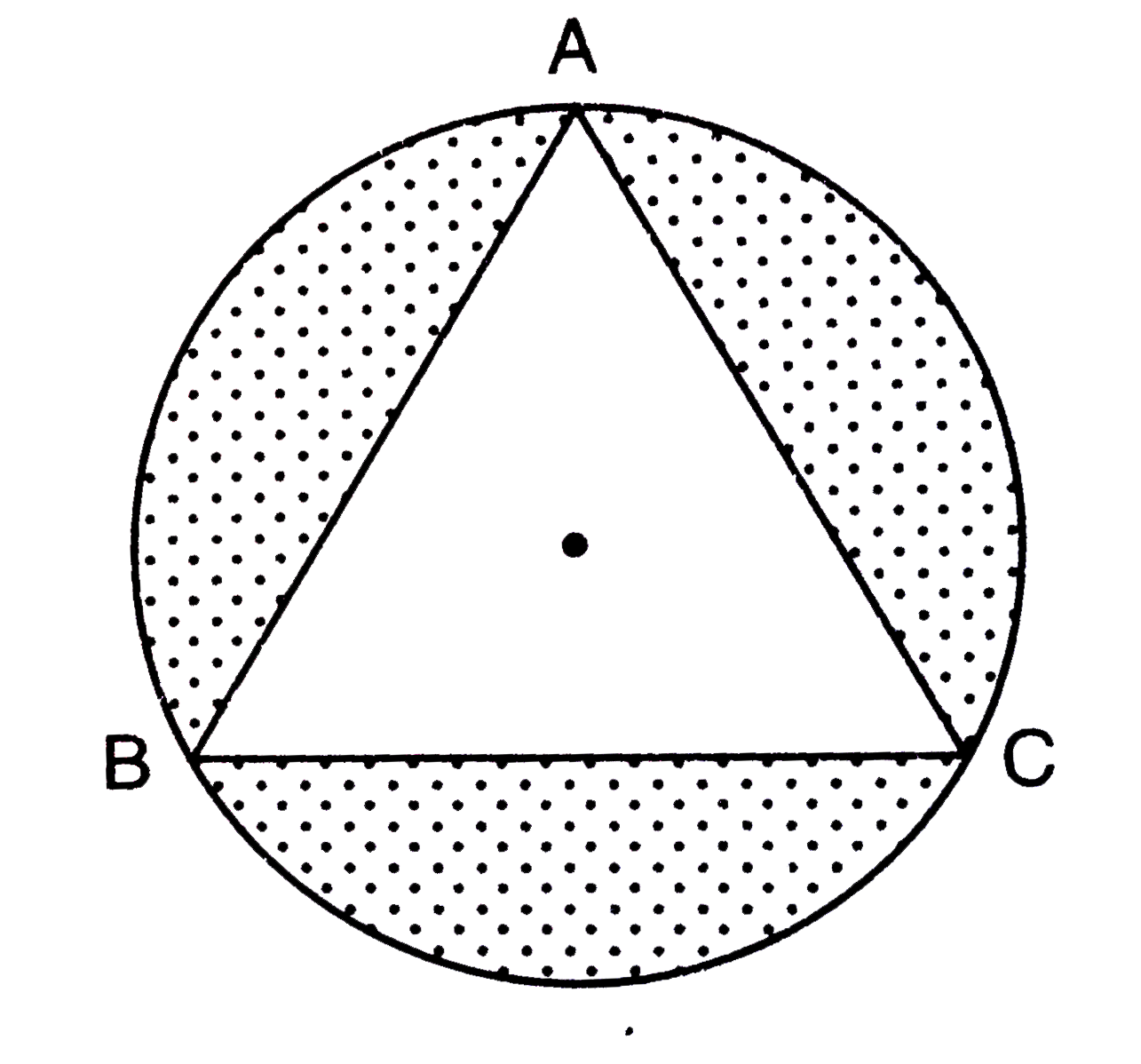 05:57View Solution
05:57View Solutionएक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 सेमी2 है । इस त्रिभुज के प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है ( देखिए आकृति )।छायांकित भाग का क्षेत्रफल ज्ञात कीजिए । ( π=3.14 और √3=1.73205 लीजिए )
 06:29View Solution
06:29View Solutionकिसी समबाहु त्रिभुज के प्रत्येक शीर्ष को केंद्र लेते हुए त्रिभुज की भुजा की आधी लम्बाई को त्रिज्या मानकर एक-एक वृत्त खींचा जाता है| त्रिभुज का जो अंश वृतों के बाहर रहता है
(i) 17320.5 वर्ग सेमी हो (π=3.14,√3=1.73205लें)
(ii) 49√3 वर्ग सेमी हो (π=227,√3=1.73)04:27View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 17300cm2 है। त्रिभुज के प्रत्येक शीर्ष को केन्द्र लेकर एक वृत्त खींचा गया ह। वृत्त की त्रिज्या समबाहु त्रिभुज की भुजा की लंबाई के आधा है । त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्त में नहीं है। (π=3.14 और √3=1.73)
06:33View Solutionचित्र में ABC एक समबाहु त्रिभुज है जिसकी एक भुजा 20 सेमी है। त्रिभुज के प्रत्येक शीर्ष से 10 सेमी त्रिज्या के वृत्त खींचे गये हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π=3.14 लीजिए)
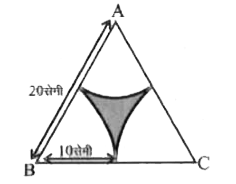 07:28View Solution
07:28View SolutionThe area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π=3.14and√3= 1.73205)
06:16View Solution

