The number of ways of factoring 91,000 into two factors, m and n, such that m>1,n>1 and gcd (m, n) = 1 is
A
7
B
15
C
32
D
37
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - SOLVED EXAMPLES (LEVEL 2) Single Correct Answer Type Questions
14 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - SOLVED EXAMPLES (LEVEL 2) Numerical Answer Type Questions
19 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
17 Videos
- PARABOLABOOK - MCGROW HILL PUBLICATIONCHAPTER - PARABOLAEXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTRE ENTRANCE EXAMINATION PAPERS
9 Videos
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Previous Years B-Architecture Entrance Examination Papers
21 Videos
Similar Questions
Knowledge Check
The number of ways of factoring 91,000 into two factors m & n such that m>1,n>1 and ged (m,n)=1 is
A70B15C32DNone of theseThe sum of all natural numbers 'n' such that 100<n<200andHCF(91,n)>1 is
A3203B3303C3221D3121The number of ways in which m men and n women can be seated in a row, so that no two women sit together is
(i) m!(m+1)!(m+n−1)!
(ii) m!(m+1)!(m−n+1)!
(iii) n!(m+1)!(m−n+1)!
(iv) m!(n+1)!(m+n−1)!A|m––|m+1–––––––∣∣m+n−1––––––––––––B|m––|m+1–––––––∣∣m−n+1––––––––––––C|n––|m+1–––––––∣∣m−n+1––––––––––––D|m––|n+1––––––∣∣m+n−1––––––––––––
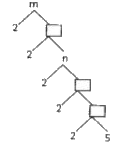
In the adjoining factor tree, find the numbers m and n

View SolutionIn which of the following, m>n(m,n∈R)?
View SolutionIn which of the following, m>n(m,n∈R)?
View SolutionThe number of solutions of the equation n−|x||m−|x∣∣=1 (where m,n>1 and n>m) is
View SolutionIf m,n are the positive integers (n>1) such that mn=121 , then value of (m−1)n+1 is :
View Solution