Let (x, y) be any point on the unit circle with centre at the origin, then
yy''−2(y')2+1=0
yy''+y'2+1=0
yy''+y'2−1=0
yy''+2y'2+1=0
The correct Answer is:B
Topper's Solved these Questions
- DIFFERENTIABILITY AND DIFFERENTIATION BOOK - MCGROW HILL PUBLICATIONCHAPTER - DIFFERENTIABILITY AND DIFFERENTIATION EXERCISE - Questions from Previous Years. AIEEE/JEE Main Papers
47 Videos
- DIFFERENTIABILITY AND DIFFERENTIATION BOOK - MCGROW HILL PUBLICATIONCHAPTER - DIFFERENTIABILITY AND DIFFERENTIATION EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
16 Videos
- DIFFERENTIABILITY AND DIFFERENTIATION BOOK - MCGROW HILL PUBLICATIONCHAPTER - DIFFERENTIABILITY AND DIFFERENTIATION EXERCISE - EXERCISE (Concept-based) Single Correct Answer Type Questions
10 Videos
- DETERMINANTSBOOK - MCGROW HILL PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - QUESTIONS FROM PREVIOUS YEARS B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
18 Videos
- DIFFERENTIAL EQUATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
14 Videos
Similar Questions
The differential equation of circles passing through the points of intersection of unit circle with centre at the origin and the line bisecting the first quadrant, is
View SolutionThe differential equation of circles passing through the points of intersection of unit circle with centre at the origin and the line bisecting the first quadrant, is
View Solution
Knowledge Check
Let A be the centre of the circle x2+y2−2x−4y−20=0. If the tangents at the points B (1, 7) and D(4,−2) on the circle meet at the point C, then the perimeter of the quadrilateral ABCD is
A60 unitsB20 unitsC40 unitsD50 units
A pair of tangents are drawn to a unit circle with centre at the origin and these tangents intersect at point P enclosing an angle of 60∘. The area enclosed by the tangents and the arc of the circle is,
View SolutionTangents are drawn to a unit circle with centre at the origin from each point on the line 2x+y=4. Then the equation to the locus of the middle point of the chord of contact is
View SolutionTangents are drawn to a unit circle with centre at the origin from each point on the line 2x+y=4. Then the equation to the locus of the middle point of the chord of contact is
View SolutionThe line y=√3x+4 touches a circle with centre at the origin. Find the radius of the circle.
View SolutionIf x+3y=0 is a tangent to the circle with centre at (-1,2) then show that the other tangent to the circle from the origin is 3x−y=0
View SolutionIf point P is located on the unit circle, then x+y=
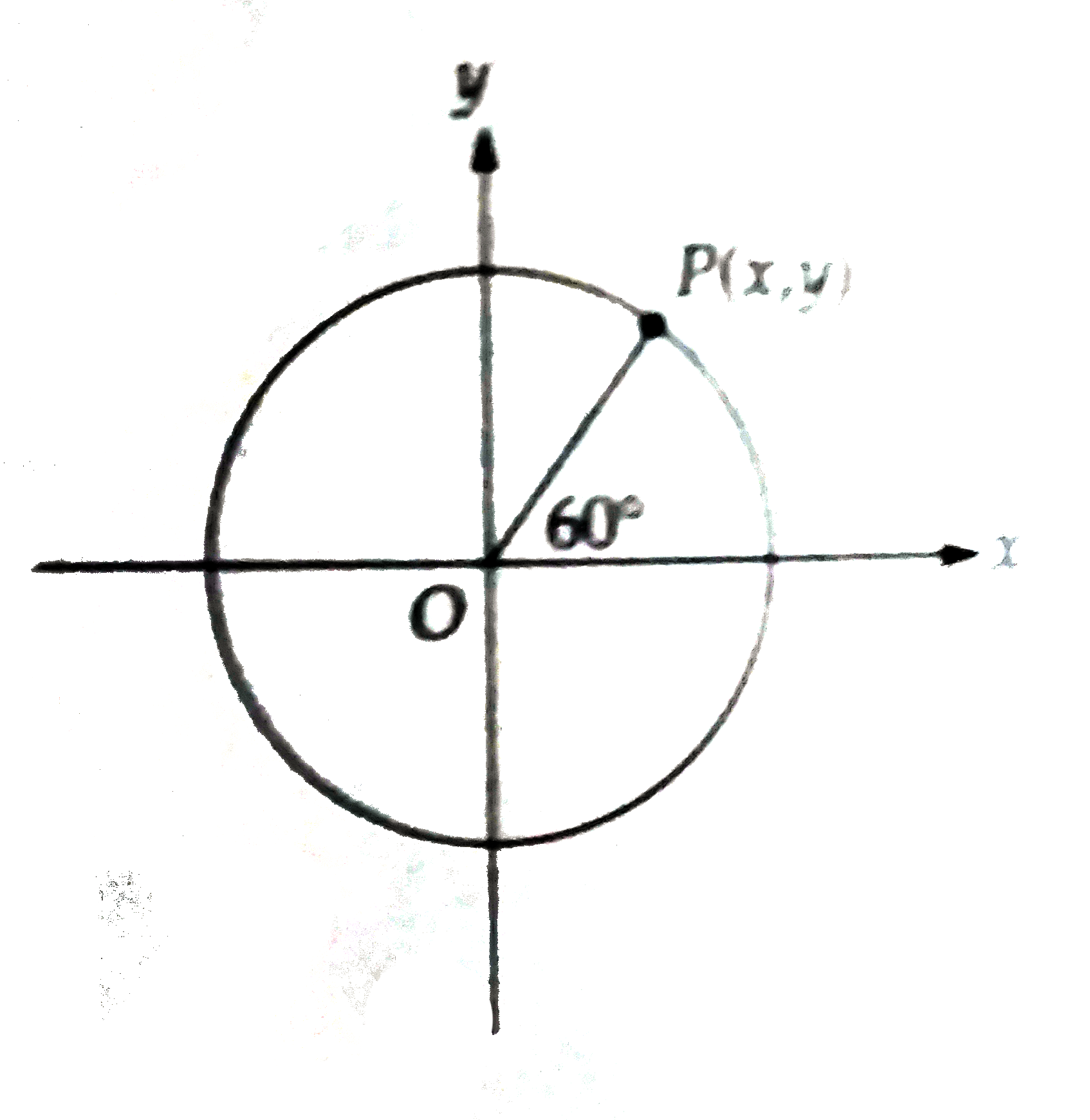
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. If the tangents at the points B (1, 7) and D(4,−2) on the circle meet at the point C, then the perimeter of the quadrilateral ABCD is
View Solution
