Let . The index n is given a positive integral value at random. The probability that the value of x will have 3 in the units place is
The correct Answer is:B
To solve the problem of finding the probability that the value of x=33n has 3 in the units place, we can follow these steps:
1. Understanding the Expression:
We start with the expression x=33n. We need to determine the units digit of x for different values of n.
2. Identifying the Units Digit:
The units digit of 33n can be determined by looking at the units digit of the base, which is 3. Therefore, we need to find the units digit of 3n.
3. Finding the Pattern in Units Digits of Powers of 3:
Let's calculate the units digits of the first few powers of 3:
- 31=3 (units digit is 3)
- 32=9 (units digit is 9)
- 33=27 (units digit is 7)
- 34=81 (units digit is 1)
- 35=243 (units digit is 3)
- 36=729 (units digit is 9)
- 37=2187 (units digit is 7)
- 38=6561 (units digit is 1)
From this, we can see that the units digits repeat every 4 terms: 3,9,7,1.
4. Determining When the Units Digit is 3:
The units digit of 3n is 3 when n≡1mod4. This means that n can take the values 1,5,9,13,… (i.e., n=4k+1 for k∈Z≥0).
5. Calculating the Probability:
Since the units digits repeat every 4 values of n, we can conclude that:
- Out of every 4 consecutive integers, there is exactly 1 integer (specifically those of the form 4k+1) that results in a units digit of 3.
Therefore, the probability P that x has a units digit of 3 is given by:
P=Number of favorable outcomesTotal outcomes=14
Final Answer:
The probability that the value of x=33n will have 3 in the units place is 14.
We start with the expression x=33n. We need to determine the units digit of x for different values of n.
The units digit of 33n can be determined by looking at the units digit of the base, which is 3. Therefore, we need to find the units digit of 3n.
Let's calculate the units digits of the first few powers of 3:
- 31=3 (units digit is 3)
- 32=9 (units digit is 9)
- 33=27 (units digit is 7)
- 34=81 (units digit is 1)
- 35=243 (units digit is 3)
- 36=729 (units digit is 9)
- 37=2187 (units digit is 7)
- 38=6561 (units digit is 1)
The units digit of 3n is 3 when n≡1mod4. This means that n can take the values 1,5,9,13,… (i.e., n=4k+1 for k∈Z≥0).
Since the units digits repeat every 4 values of n, we can conclude that:
- Out of every 4 consecutive integers, there is exactly 1 integer (specifically those of the form 4k+1) that results in a units digit of 3.
P=Number of favorable outcomesTotal outcomes=14
The probability that the value of x=33n will have 3 in the units place is 14.
Similar Questions
If n is a positive integer then the probability that 3n has 3 at unit place is
View SolutionThere are n letters and n addressed envelopes . If the letters are placed in the envelopes at random , what is the probability that all the letters are not placed in the right evelope ?
View SolutionFor how many positive integral values of n does n! end with precisely 25 zeros?
View SolutionThe smallest positive integral value of n for which (1+√3i)n2 is real is
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionThe probability of a random variable X is given below
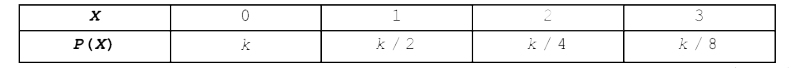
Determine the value of k
View SolutionThe least integral value of x for which 33−x(2+3x)>0 is
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View Solution
