Find the velocity of photoelectrons liberated by electromagnetic radiation of wavelength $λ = 18.0 n m$ from stationary $H e^{+}$ ions in the ground state.

$2.3 \times 10^{6} m s^{- 1}$

$1.3 \times 10^{6} m s^{- 1}$

$2.3 \times 10^{5} m s^{- 1}$

$1.3 \times 10^{3} m s^{- 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video & image solution for Find the velocity of photoelectrons liberated by electromagnetic radiation of wavelength lambda=18.0nm from stationary He^(+) ions in the ground state. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS JEE MOCK TEST 6

Similar Questions

Suppose the energy liberated in the in the recombination of a hole-electron pair is converted into electromagnetic radiation.If the maximum wavelength emmited is 820nm,What is the band gap?
View Solution
Ground state energy of H-atom is $(- E_{1})$ ,t he velocity of photoelectrons emitted when photon of energy $E_{2}$ strikes stationary $L i^{2 +}$ ion in ground state will be:
View Solution
The electrical conductivity of a semiconductor increases when electromagnetic radiation of wavelength shorter than 2480 nm is incident on it. Find the band gap of the semiconductor.
View Solution
The hydrogen atom in ground state is excited by a monochromatic radiation of wavelength $λ = 1025 A$ . The possible number of emmision spectral lines in the spectrum will be (hc = 12400 eV A)
View Solution
In a hydragen spectrum third line of Balmer's series having wavelength $λ$ . Find the binding energy o the ground state.
View Solution
The energy required to stop ejection of electrons from a Cu plate is $0.24 e V$ .Calculate the work function Cu when a radiation of wavelength $λ = 250$ nm strikes the plate
View Solution
In a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state $(n = 1)$ are shown in the energy level diagram

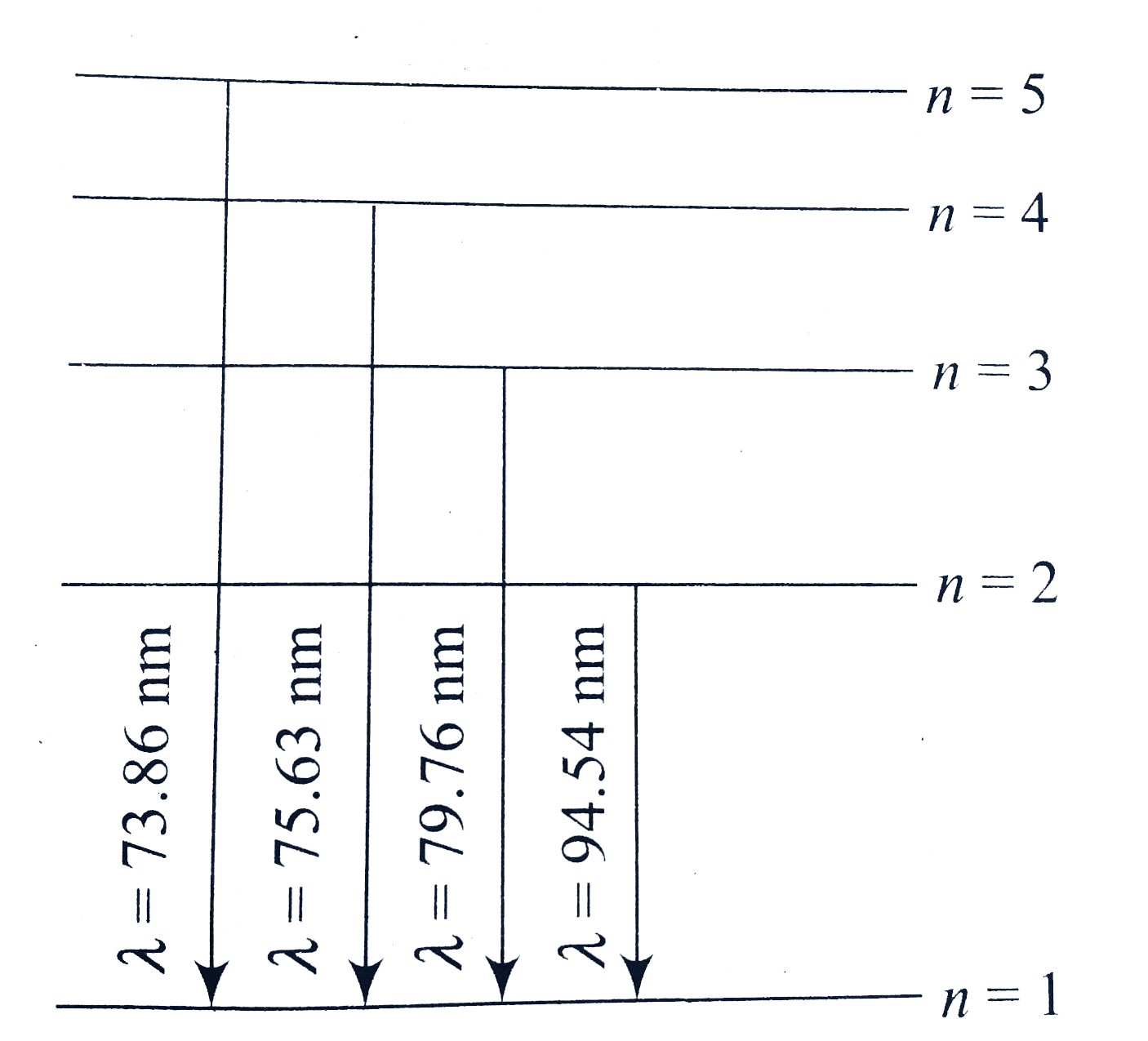
$λ_{5 \to 1} = 73.86 n m$
$λ_{4 \to 1} = 75.63 n m$
$λ_{3 \to 1} = 79.76 n m$
$λ_{2 \to 1} = 94.54 n m$
The energy of the atom in level $n = 1$ is nearly
View Solution
In a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state $(n = 1)$ are shown in the energy level diagram

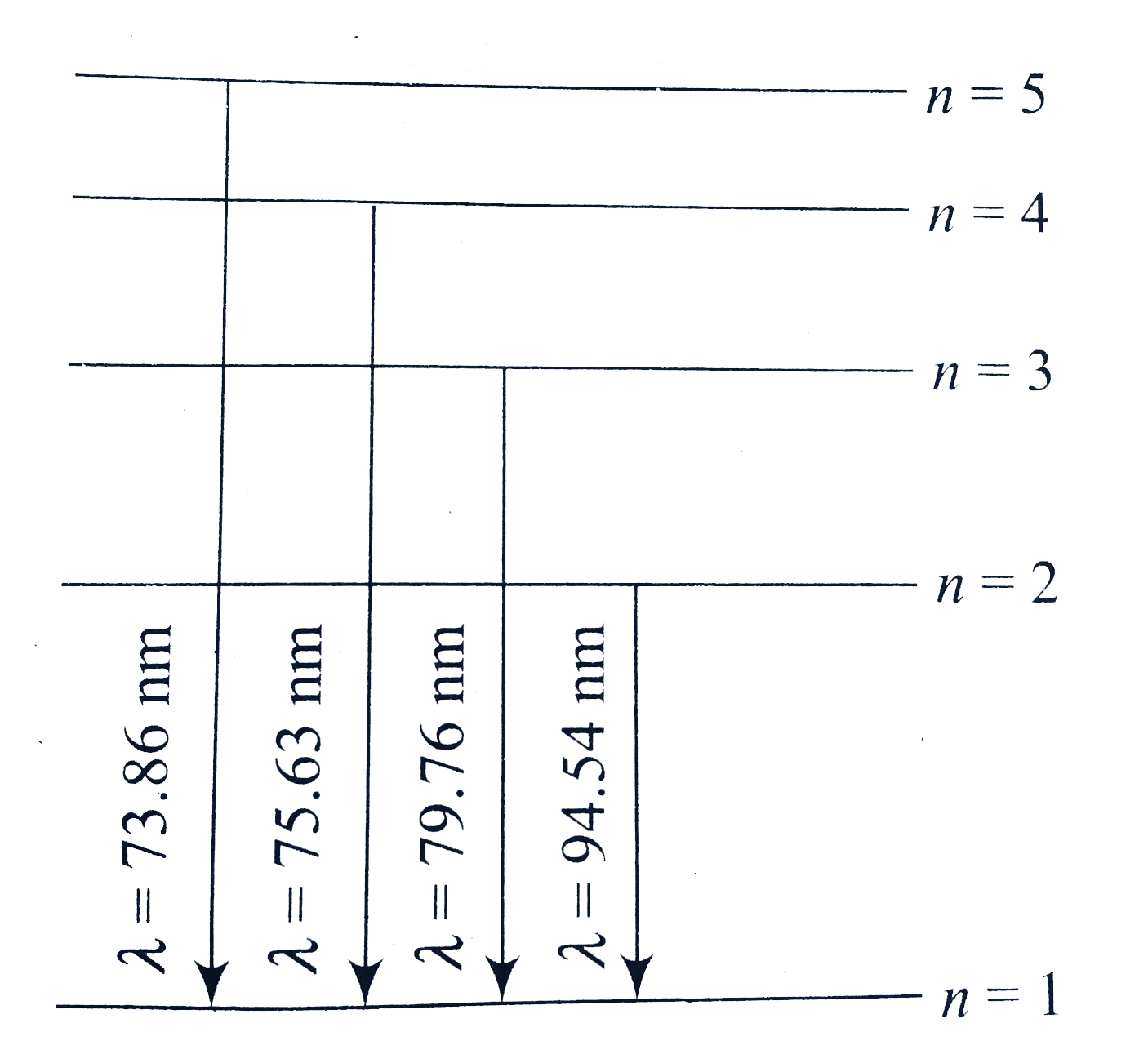
$λ_{5 \to 1} = 73.86 n m$
$λ_{4 \to 1} = 75.63 n m$
$λ_{3 \to 1} = 79.76 n m$
$λ_{2 \to 1} = 94.54 n m$
The possible energy of the atom in $n = 3$ cannot be
View Solution
Photoelectrons ar ejected from a surface when light of wavelenght $λ_{1} = 550 n m$ is incident on it. The stopping potential for such electrons is $λ_{S 1} = 0.19 V$ . Suppose that radiation of wavelength $λ_{2} = 190 n m$ is incident of the surface.
Q. Calculate the stopping potential $V_{S 2}$ .
View Solution
Photoelectrons ar ejected from a surface when light of wavelenght $λ_{1} = 550 n m$ is incident on it. The stopping potential for such electrons is $λ_{S 1} = 0.19 V$ . Suppose that radiation of wavelength $λ_{2} = 190 n m$ is incident of the surface.
Q. Calulate the work function of the surface.
View Solution

Find the velocity of photoelectrons liberated by electromagnetic radiation of wavelength λ=18.0nm from stationary He+ ions in the ground state.

The correct Answer is:A

Similar Questions

Recommended Questions

Find the velocity of photoelectrons liberated by electromagnetic radiation of wavelength $λ = 18.0 n m$ from stationary $H e^{+}$ ions in the ground state.