The moment of inertial of a rigid body in terms of its angular momentum L and kinetic energy K is
L2K
L22K
L2K2
L2K
The correct Answer is:B
Step by step video & image solution for The moment of inertial of a rigid body in terms of its angular momentum L and kinetic energy K is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
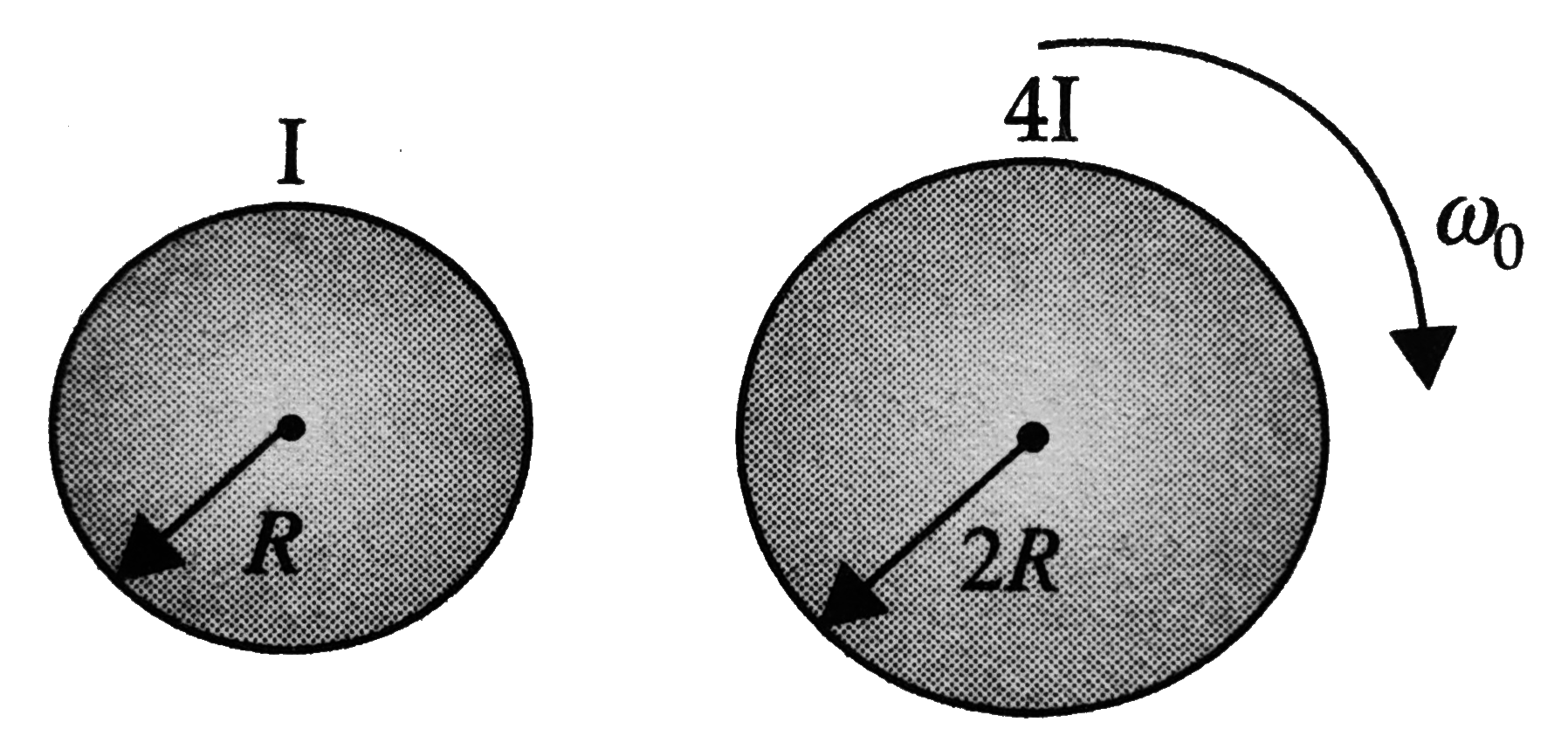
Two cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
View SolutionThe moment of inertia (I) and the angular momentum (L) are related by the expression
View Solution
Knowledge Check
Assertion : The moment of inertia of a rigid body reduces to its minimum value, when the axis of rotation passes through its centre of gravity.
Reason : The weight of a rigid body always acts through its centre of gravity.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.
A particle of mass m has momentum p. Its kinetic energy will be
View SolutionThe angular momentum of body remains conserve if :
View SolutionBy keeping moment of inertia of a body constant, if we double the time period, then angular momentum of body
View SolutionThe dimensions of (angular momentum)/(magnetic moment) are
View SolutionDerive an expression for the magnetic moment (→μ) of an electron revolving around the nucleus in termsof its angular momentum (→l). What is the direction of the magnetic moment of the electron with respect to its angular momentum?
View SolutionThe ratio of magnetic dipole moment to angular momentum of electron is
View SolutionKeeping moment of inertia constant, the angular momentum of a body is increased by 20%. The percentage increase in its rotational kinetic energy is
View Solution