The equivalent conductivity of 0.1M weak acid is 100 times less than that at infinite dilution. The degree of dissociation of weak electrolyte at 0.1M is.
100
10
0.01
0.001
The correct Answer is:C
To find the degree of dissociation of a weak electrolyte at a concentration of 0.1M, we can follow these steps:
Step 1: Understand the relationship between equivalent conductivity at different concentrations
The problem states that the equivalent conductivity of the 0.1M weak acid is 100 times less than that at infinite dilution. We can express this relationship mathematically:
\(
\Lambda_{eq} = \frac{\Lambda_{\infty}}{100}
\)
where:
- \(\Lambda_{eq}\) = equivalent conductivity at 0.1M
- \(\Lambda_{\infty}\) = equivalent conductivity at infinite dilution
Step 2: Use the formula for degree of dissociation
The degree of dissociation (\(\alpha\)) of a weak electrolyte can be calculated using the formula:
\(
\alpha = \frac{\Lambda_{eq}}{\Lambda_{\infty}}
\)
Step 3: Substitute the value of \(\Lambda_{eq}\)
From Step 1, we know that:
\(
\Lambda_{eq} = \frac{\Lambda_{\infty}}{100}
\)
Now, substitute this value into the formula for \(\alpha\):
\(
\alpha = \frac{\frac{\Lambda_{\infty}}{100}}{\Lambda_{\infty}}
\)
Step 4: Simplify the equation
When we simplify the above equation, we get:
\(
\alpha = \frac{1}{100}
\)
or
\(
\alpha = 0.01
\)
Conclusion
Thus, the degree of dissociation of the weak electrolyte at 0.1M is 0.01.
---
The problem states that the equivalent conductivity of the 0.1M weak acid is 100 times less than that at infinite dilution. We can express this relationship mathematically:
\Lambda_{eq} = \frac{\Lambda_{\infty}}{100}
\)
- \(\Lambda_{eq}\) = equivalent conductivity at 0.1M
- \(\Lambda_{\infty}\) = equivalent conductivity at infinite dilution
The degree of dissociation (\(\alpha\)) of a weak electrolyte can be calculated using the formula:
\alpha = \frac{\Lambda_{eq}}{\Lambda_{\infty}}
\)
From Step 1, we know that:
\Lambda_{eq} = \frac{\Lambda_{\infty}}{100}
\)
\alpha = \frac{\frac{\Lambda_{\infty}}{100}}{\Lambda_{\infty}}
\)
When we simplify the above equation, we get:
\alpha = \frac{1}{100}
\)
\alpha = 0.01
\)
Thus, the degree of dissociation of the weak electrolyte at 0.1M is 0.01.
Similar Questions
At infinite dilution, the percentage dissociation of both weak acid and weak base is:
View SolutionThe specific conductance of a0.5 N solution of an electrolyte at 25∘C is 0.00045 Scm−1 . The equivalent conductance of this electrolyte at infinite dilution is 300 S cm2eq−1 . The degree of dissociation of the electrolyte is
View Solution
Knowledge Check
Assertion:Kohlrausch law helps to find the molar conductivity of weak electrolyte at infinite dilution.
Reason:Molar conductivity of a weak electrolyte at infinite dilution cannot be determined experimentally.AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explanation of assertion .CIf assertion is true but reason is false .DIf both assertion and reason are false .
On diluting aqueous solution of weak electrolyte to 100 times
View SolutionThe equivalent conductance of M/32 solution of a weak monobasic acid is 8.0 and at infinite dilution is 400. The dissociation constant of this acid is :
View SolutionThe equivalent conductance of M20solution of a weak
monobasic acid is 10 mhos cm2 and at infinite dilution is 200 mhos cm2. The dissociation consant of this acid is :-
View Solution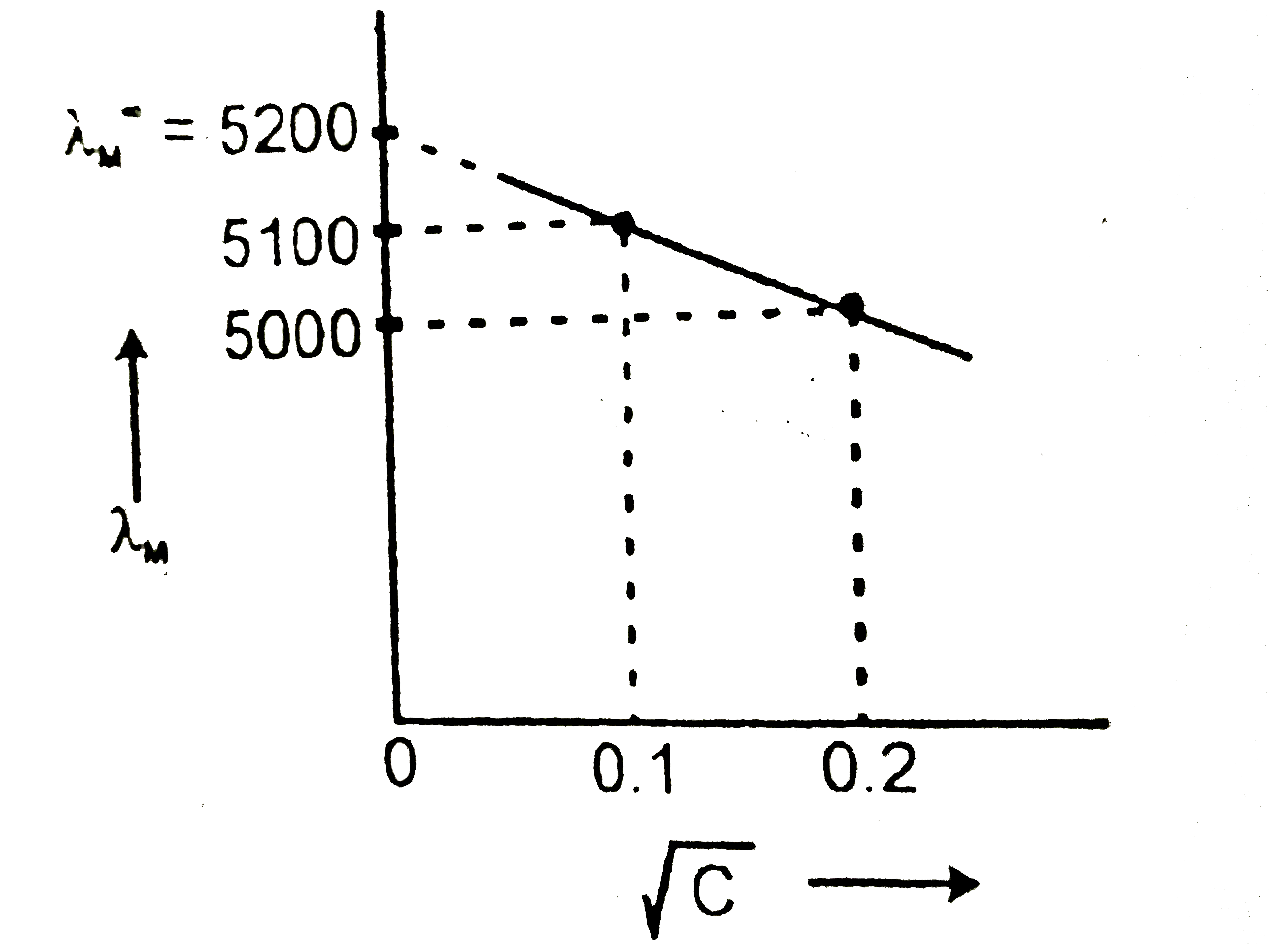
At 0.04 M concentration the molar conductivity of a solution of a electrolyte is 5000Ω−1cm2mol−1 while at 0.01 M concentration the value is 5100Ω−1cm2mol−1 making necessary assumption (taking it as strong electrolyte) find the molar conductivity at infinite dilution and also determine the degree of dissociation of strong electrolyte at 0.04M.
View SolutionThe increase in equivalent conductivity of a weak electrolyte with dilution is due to :
View SolutionHA is a weak acid. The pH of 0.1 M HA solution is 2. What is the degree of dissociation (α) of HA ?
View SolutionEquivalent conductane of 0.1 M HA (weak acid) solution is 10 Scm2equivalent−1 and that at infinite dilution is 200 S cm2 equivalent−1 Hence pH of HA solution is
View Solution
