A stone is thrown at 25m/s at 53∘ above the horizontal. At what time its velocity is at 45∘ below the horizontal?
0.5s
4s
3.5s
2.5s
The correct Answer is:C
To solve the problem, we need to analyze the motion of the stone thrown at an angle. We'll break it down step by step.
Step 1: Determine the initial velocity components
The stone is thrown with an initial velocity u=25m/s at an angle θ=53∘ above the horizontal.
- The horizontal component of the initial velocity (ux):
ux=ucos(θ)=25cos(53∘)
Using cos(53∘)≈35:
ux=25×35=15m/s
- The vertical component of the initial velocity (uy):
uy=usin(θ)=25sin(53∘)
Using sin(53∘)≈45:
uy=25×45=20m/s
Step 2: Analyze the velocity at 45 degrees below the horizontal
At the time we want to find, the stone's velocity is at 45∘ below the horizontal. This means the horizontal and vertical components of the velocity are equal in magnitude but opposite in direction.
Let V be the magnitude of the velocity at this point. The horizontal component (Vx) is:
Vx=Vcos(45∘)=V1√2
And since the horizontal component remains constant:
Vx=ux=15m/s
From this, we can find V:
V1√2=15⟹V=15√2m/s
Step 3: Find the vertical component of the velocity
The vertical component of the velocity when the stone is at 45∘ below the horizontal is:
Vy=−Vsin(45∘)=−V1√2
Substituting V:
Vy=−15√21√2=−15m/s
Step 4: Use the kinematic equation to find the time
We can use the kinematic equation for vertical motion:
Vy=uy−gt
Substituting the known values:
−15=20−10t
Rearranging gives:
10t=20+15⟹10t=35⟹t=3.5s
Final Answer
The time at which the stone's velocity is at 45∘ below the horizontal is t=3.5s.
---
The stone is thrown with an initial velocity u=25m/s at an angle θ=53∘ above the horizontal.
ux=ucos(θ)=25cos(53∘)
Using cos(53∘)≈35:
ux=25×35=15m/s
uy=usin(θ)=25sin(53∘)
Using sin(53∘)≈45:
uy=25×45=20m/s
At the time we want to find, the stone's velocity is at 45∘ below the horizontal. This means the horizontal and vertical components of the velocity are equal in magnitude but opposite in direction.
Vx=Vcos(45∘)=V1√2
And since the horizontal component remains constant:
Vx=ux=15m/s
V1√2=15⟹V=15√2m/s
The vertical component of the velocity when the stone is at 45∘ below the horizontal is:
Vy=−Vsin(45∘)=−V1√2
Substituting V:
Vy=−15√21√2=−15m/s
We can use the kinematic equation for vertical motion:
Vy=uy−gt
Substituting the known values:
−15=20−10t
Rearranging gives:
10t=20+15⟹10t=35⟹t=3.5s
The time at which the stone's velocity is at 45∘ below the horizontal is t=3.5s.
Similar Questions
A body is thrown with some velocity from the ground. Maximum height when it is thrown at 60∘ to horizontal is 90m. What is the height reached when it is thrown at 30∘ to the horizontal:-
View SolutionA projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View Solution
Knowledge Check
A cricket ball is thrown at a speed of 30 m s−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
A2 sB3 sC4 sD5 s
An object is being thrown at a speed of 20 m/s in a direction 45∘ above the horizontal . The time taken by the object to return to the same level is
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA stone is thrown at an angle of 45∘ to the horizontal with kinetic energy K. The kinetic energy at the highest point is
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
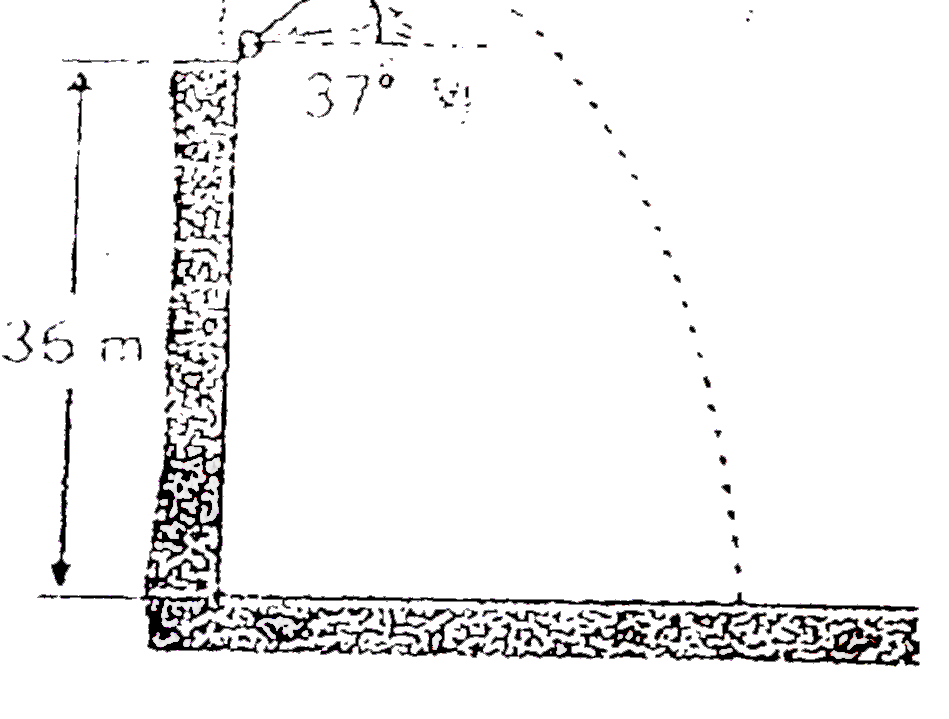 :
:
View Solution(b) A stone is thrown from a bridge at an angle of 30∘ down with the horizontal with a velocity of 25 m//s . If the stone strikes the water after 2.5 seconds then calculate the height of the bridge from the water surface (g=9.8m/s2).
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View Solution
