If A is the amplitude of the wave coming from a line source at a distance r, then :
A∝r−12
A∝r−1
A∝r2
A∝r1
The correct Answer is:B
To solve the problem, we need to establish the relationship between the amplitude A of a wave coming from a line source and the distance r from that source.
1. Understanding the Source Types:
- We differentiate between a point source and a line source. A point source radiates in all directions, while a line source emits waves along its length.
2. Amplitude and Intensity Relationship:
- For a point source, the intensity I is inversely proportional to the square of the distance r:
I∝1r2
- The amplitude A is related to intensity by:
A∝√I
- Therefore, for a point source:
A∝√1r2⇒A∝1r
3. For a Line Source:
- For a line source, the intensity I is inversely proportional to the distance r:
I∝1r
- Again, using the relationship between amplitude and intensity:
A∝√I
- Thus, for a line source:
A∝√1r⇒A∝1√r⇒A∝r−1/2
4. Conclusion:
- Therefore, the amplitude A of the wave coming from a line source at a distance r can be expressed as:
A∝r−1/2
- This means that the correct answer is that the amplitude varies as r−1/2.
Final Answer:
The amplitude A varies as r−1/2.
- We differentiate between a point source and a line source. A point source radiates in all directions, while a line source emits waves along its length.
- For a point source, the intensity I is inversely proportional to the square of the distance r:
I∝1r2
- The amplitude A is related to intensity by:
A∝√I
- Therefore, for a point source:
A∝√1r2⇒A∝1r
- For a line source, the intensity I is inversely proportional to the distance r:
I∝1r
- Again, using the relationship between amplitude and intensity:
A∝√I
- Thus, for a line source:
A∝√1r⇒A∝1√r⇒A∝r−1/2
- Therefore, the amplitude A of the wave coming from a line source at a distance r can be expressed as:
A∝r−1/2
- This means that the correct answer is that the amplitude varies as r−1/2.
The amplitude A varies as r−1/2.
Similar Questions
Knowledge Check
Two light waves superimposing at the mid-point of the screen are coming from coherent sources of light with phase difference 3pi rad. Their amplitudes are 1 cm each. The resultant amplitude at the given point will be.
A5 cmB3 cmC2 cmDzero
The intensity of a wave emitted from a small source at a distance 10 m is 20×10−3Wm−2. What is the intensity at a distance 100 m ?
View SolutionStatement-1: Two separate sources of light giving out light of the same frequency do not produce sustained interference.
Statement-2 : The amplitude of the waves from the sources are never equal.
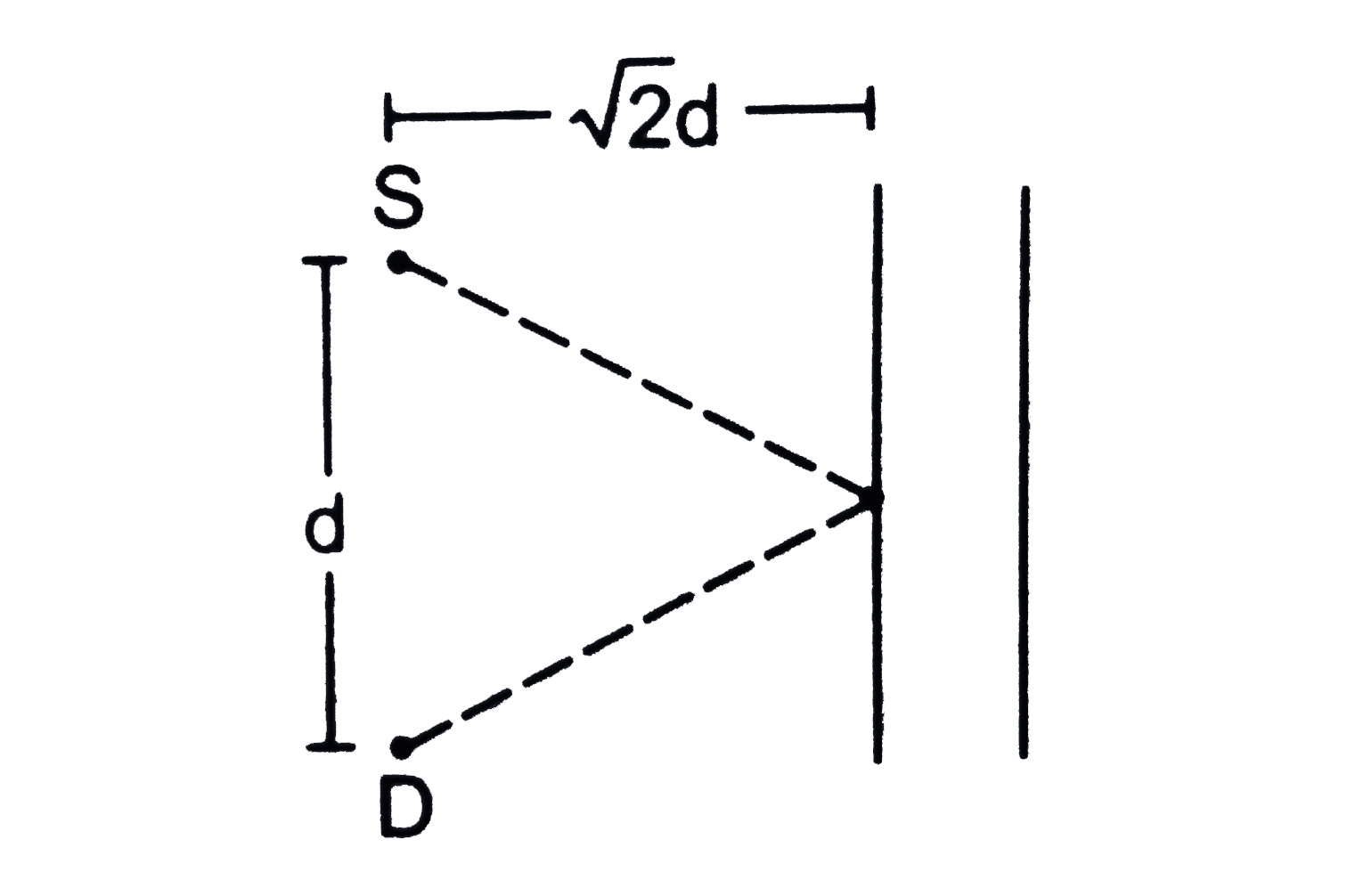
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
View SolutionAt a distance 20m from a point source of sound the loudness level is 30dB. Neglecting the damping, find
(a) the loundness at 10m from the source
(b) the distance from the source at which sound is not heard.
View SolutionA strain of sound waves is propagated along an organ pipe and gets reflected from an open end . If the displacement amplitude of the waves (incident and reflected) are 0.002cm , the frequency is 1000Hz and wavelength is 40cm. Then , the displacement amplitude of vibration at a point at distance 10cm from the open end , inside the pipe is
View Solutionshow that when reflection takes place from a boundary separating two media and the velocity in the second medium is infinitely large , the amplitude of the reflected wave is equal to the amplitude of the incident wave and there is a phase change of π in the displacement wave.
View SolutionIntensity due to line source S1 at a distance of r is I0 and intensity due to other line source S2 at a distance of r is 4I0 and frequency of both source are equal. If interference occurs at a point P as shown in the figure and wavelength of both sources is r, find the resultant intensity (in wa/m2) at P. (where I0=2watt/m2)

View Solution
