A gas is present in a cylinder fitted with movable piston. Above and below the piston there is equal number of moles of gas. The volume above is two times the volume below at a temperature of 300 K. At what temperature will the volume above be four times the volume below-
600 K
400 K
200 K
120 K
The correct Answer is:D
To solve the problem, we need to analyze the situation using the ideal gas law and the relationship between temperature and volume for a gas under constant pressure conditions.
1. Understanding the Initial Conditions:
- We have a cylinder with a movable piston.
- The volume above the piston (V_upper) is 2V, and the volume below the piston (V_lower) is V.
- The initial temperature (T_initial) is 300 K.
- The number of moles of gas (n) is equal above and below the piston.
2. Setting Up the Final Condition:
- We need to find the final temperature (T_final) when the volume above the piston becomes four times the volume below the piston.
- Therefore, the new volume above the piston (V_upper_final) will be 4V, and the volume below the piston (V_lower_final) remains V.
3. Applying the Ideal Gas Law:
- The ideal gas law states that PV=nRT.
- Since the pressure (P) is constant (due to the movable piston), we can relate the initial and final states using the formula:
TinitialVinitial=TfinalVfinal
4. Substituting the Known Values:
- For the initial state:
- Tinitial=300K
- Vinitial=Vupper=2V
- For the final state:
- Tfinal=?
- Vfinal=Vupper_final=4V
5. Setting Up the Equation:
- Plugging in the values into the equation:
3002V=Tfinal4V
6. Solving for T_final:
- Cancel out the common volume (V) from both sides:
3002=Tfinal4
- This simplifies to:
150=Tfinal4
- Now, multiply both sides by 4 to find Tfinal:
Tfinal=150×4=600K
Final Answer:
The temperature at which the volume above the piston will be four times the volume below is 600 K.
- We have a cylinder with a movable piston.
- The volume above the piston (V_upper) is 2V, and the volume below the piston (V_lower) is V.
- The initial temperature (T_initial) is 300 K.
- The number of moles of gas (n) is equal above and below the piston.
- We need to find the final temperature (T_final) when the volume above the piston becomes four times the volume below the piston.
- Therefore, the new volume above the piston (V_upper_final) will be 4V, and the volume below the piston (V_lower_final) remains V.
- The ideal gas law states that PV=nRT.
- Since the pressure (P) is constant (due to the movable piston), we can relate the initial and final states using the formula:
TinitialVinitial=TfinalVfinal
- For the initial state:
- Tinitial=300K
- Vinitial=Vupper=2V
- For the final state:
- Tfinal=?
- Vfinal=Vupper_final=4V
- Plugging in the values into the equation:
3002V=Tfinal4V
- Cancel out the common volume (V) from both sides:
3002=Tfinal4
- This simplifies to:
150=Tfinal4
- Now, multiply both sides by 4 to find Tfinal:
Tfinal=150×4=600K
The temperature at which the volume above the piston will be four times the volume below is 600 K.
Similar Questions
Knowledge Check
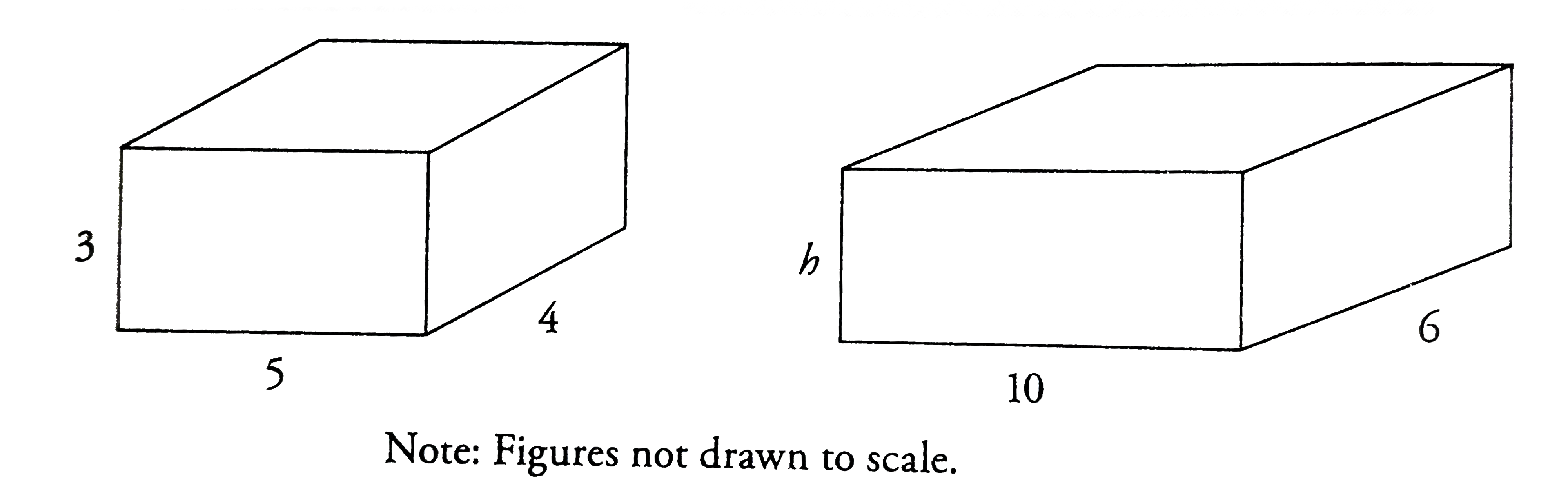 If the volumes of the two boxes above are equal, what is the value of h?A1B2C4D5
If the volumes of the two boxes above are equal, what is the value of h?A1B2C4D5
What is the volume of a gas at absolute zero of temperature ?
View SolutionIf the volume of a given mass of a gas at constant temperature becomes one third times, the pressure will be
View SolutionThe volume of a given mass of a gas at 15∘C is 100 cm3 To what temperature should it be To what temperature should it be volume of 125 cm3
View SolutionInitial volume of a gas is 1L at temperature 100K. What is the volume of a gas at 300K.
View SolutionThe volume of a given mass of gas is 20 litre at 300K and 1 atmosphere pressure .At what pressure will the volume of the gas be 1 litre at the same temperature ?
View SolutionIf the volume of a given mass of a gas at constant temperature becomes three times, the pressure will be
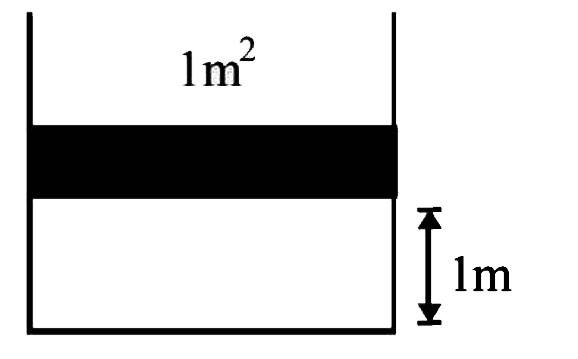
View SolutionA diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
View Solution
