A screen is placed 90 cm from an object. The image an object on the screen is formed by a convex lens two different locations separated by 20 cm. the focal length of the lens is
18 cm
21.4 cm
60 cm
85.6 cm
The correct Answer is:B
To solve the problem, we need to determine the focal length of a convex lens given the distance between an object and a screen, along with the information about the two positions of the lens.
1. Understanding the Setup:
- The distance from the object to the screen is given as 90 cm.
- The two positions of the lens create images on the screen that are 20 cm apart.
2. Setting Up the Equations:
- Let u1 be the object distance for the first position of the lens and v1 be the image distance for the first position.
- According to the problem, we have:
u1+v1=90(1)
- For the second position of the lens, let u2 and v2 be the object and image distances, respectively. Since the lens is moved 20 cm, we can express this as:
v1−u1=20(2)
3. Solving the Equations:
- From equation (1), we can express v1 in terms of u1:
v1=90−u1(3)
- Substitute equation (3) into equation (2):
(90−u1)−u1=20
90−2u1=20
2u1=70
u1=35cm
- Now substitute u1 back into equation (3) to find v1:
v1=90−35=55cm
4. Using the Lens Formula:
- The lens formula is given by:
1f=1v−1u
- Substitute v1 and u1 into the lens formula:
1f=155−1−35
1f=155+135
- To combine these fractions, find a common denominator (which is 385):
1f=7385+11385=18385
- Therefore, the focal length f is:
f=38518≈21.4cm
Final Answer:
The focal length of the lens is approximately 21.4 cm.
- The distance from the object to the screen is given as 90 cm.
- The two positions of the lens create images on the screen that are 20 cm apart.
- Let u1 be the object distance for the first position of the lens and v1 be the image distance for the first position.
- According to the problem, we have:
u1+v1=90(1)
- For the second position of the lens, let u2 and v2 be the object and image distances, respectively. Since the lens is moved 20 cm, we can express this as:
v1−u1=20(2)
- From equation (1), we can express v1 in terms of u1:
v1=90−u1(3)
- Substitute equation (3) into equation (2):
(90−u1)−u1=20
90−2u1=20
2u1=70
u1=35cm
- Now substitute u1 back into equation (3) to find v1:
v1=90−35=55cm
- The lens formula is given by:
1f=1v−1u
- Substitute v1 and u1 into the lens formula:
1f=155−1−35
1f=155+135
- To combine these fractions, find a common denominator (which is 385):
1f=7385+11385=18385
- Therefore, the focal length f is:
f=38518≈21.4cm
The focal length of the lens is approximately 21.4 cm.
Similar Questions
An object is placed 50cm from a screen as shown in figure.
A converging lens is moved such that line MN is its principal axis. Sharp images are formed on the screen in two positions of lens separated by 30cm. Find the focal length of the lens in cm.

View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View Solution
Knowledge Check
A screen is placed 90cm from an object. The image of the object on the screen is formed by a convex lens at two different location separated by 20cm. Determine the focal length of the lens.
A42.8cmB21.4cmC10.7cmD5.5cmAn object is placed at a distance of 1.5m from a screen and a convex lens is interposed between them. The magnification produced is 4. What is the focal length of the lens ?
A1mB0.5mC0.24mD2m
Find the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionA convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View SolutionA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
View SolutionA point object is placed at a distance of 15 cm from a convex lens. The image is formed on the other side at a distance of 30 cm from the lens. When a concave lens is placed in contact with the convex lens, the image shifts away further by 30 cm. Calculate the focal lengths of the two lenses.
View SolutionAn object is placed 30cm away from a convex lens of focal length 10cm and a sharp image is formed on a screen. Now, a convex lens is placed In contact with the convex lens. The screen now has to be moved by 45cm to get a sharp image again. The magnitude of focal length of the convex lends in (in cm)
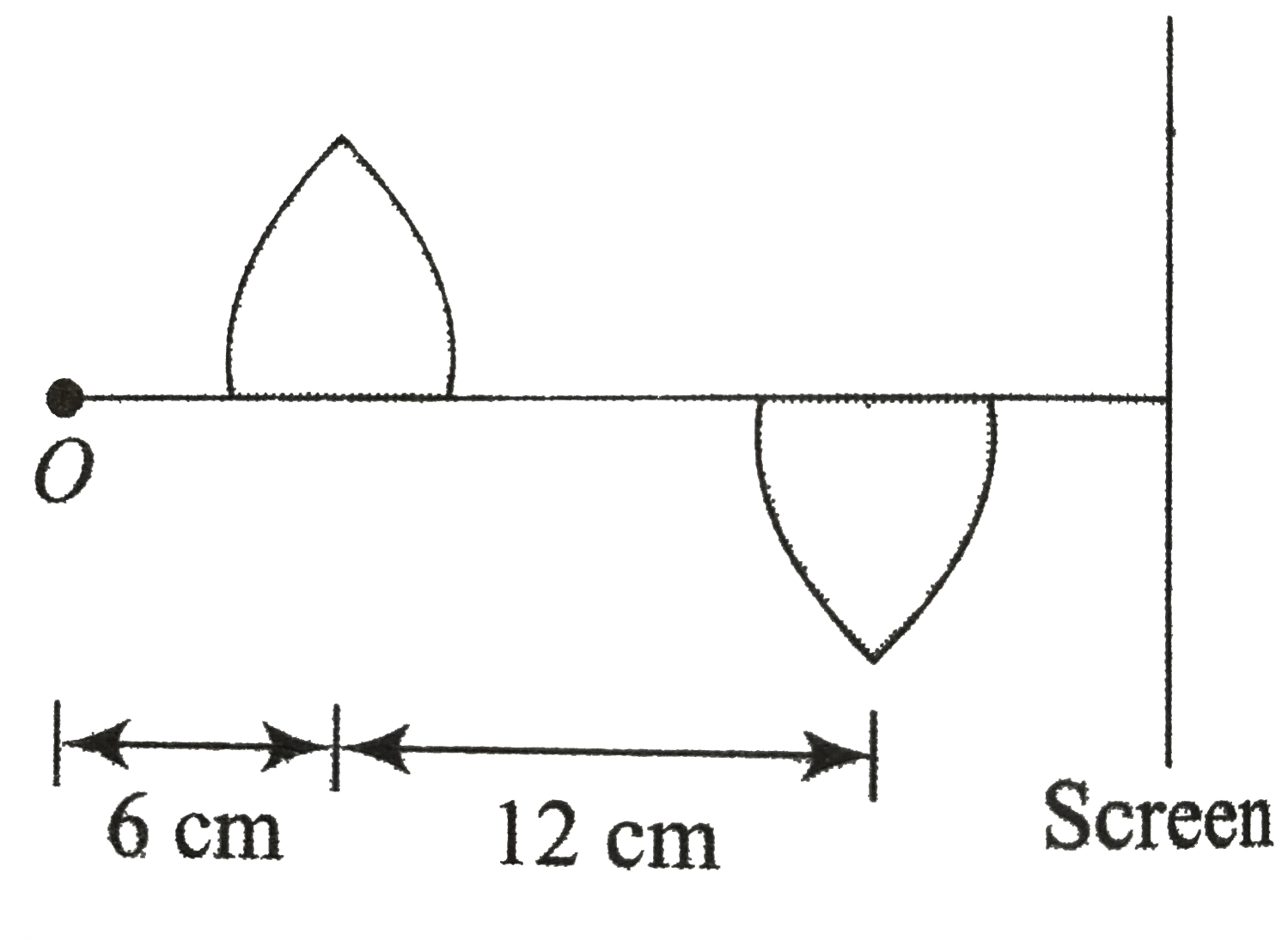
View SolutionA convex lens is cut in half along its principal axis and the two halves are separated by a distance of 12cm. An object is placed 6cm in front of the lens as shown in Figure., Two sharp images are formed on the screen placed 80cm from the object. What is the focal length of the lens?
View Solution
