A point P lies on the axis of a flat coil carryinga current. The mangetc moment of the coil is μ. What will be the magnetic field at point P ? It is given that the distance of P from the centre of coil is d, which is large compared to the radius of the coil.
μ02π(μd3)
μ04π(μd3)
μ06π(μd2)
μ08π(μd2)
The correct Answer is:A
To find the magnetic field at point P, which lies on the axis of a flat coil carrying a current, we can follow these steps:
1. Understanding the Setup:
- We have a flat circular coil of radius r carrying a current I.
- The magnetic moment μ of the coil is given.
- The point P is located at a distance d from the center of the coil along its axis, where d is much larger than r (i.e., d≫r).
2. Magnetic Field Due to a Small Element:
- Consider a small current element dl on the coil. The magnetic field dB at point P due to this element can be expressed using the Biot-Savart Law:
dB=μ0Idl4πr2
- Here, r is the distance from the current element to point P, which can be approximated as:
r=√d2+r2
- However, since d≫r, we can simplify this to:
r≈d
3. Components of the Magnetic Field:
- The magnetic field has both vertical and horizontal components. The vertical components from opposite sides of the coil will cancel each other out, leaving only the horizontal component.
- The horizontal component of the magnetic field dBh can be expressed as:
dBh=dB⋅cos(θ)
- Using the small angle approximation, where θ is the angle between the radius of the coil and the line connecting the current element to point P, we can express cos(θ) in terms of r/d.
4. Integrating Over the Coil:
- To find the total magnetic field B at point P, we need to integrate dBh over the entire coil:
B=∫dBh=∫μ0Idl⋅cos(θ)4πd2
- The total length of the coil is 2πr, and we can substitute dl with rdθ to perform the integration.
5. Substituting Magnetic Moment:
- The magnetic moment μ of the coil is defined as:
μ=I⋅A=I⋅πr2
- We can express I in terms of μ:
I=μπr2
6. Final Expression for Magnetic Field:
- Substituting I back into the expression for B and simplifying gives:
B=μ0μ2πd3
- This is the magnetic field at point P, where d is much larger than the radius of the coil.
Final Answer:
The magnetic field at point P is given by:
B=μ0μ2πd3
- We have a flat circular coil of radius r carrying a current I.
- The magnetic moment μ of the coil is given.
- The point P is located at a distance d from the center of the coil along its axis, where d is much larger than r (i.e., d≫r).
- Consider a small current element dl on the coil. The magnetic field dB at point P due to this element can be expressed using the Biot-Savart Law:
dB=μ0Idl4πr2
- Here, r is the distance from the current element to point P, which can be approximated as:
r=√d2+r2
- However, since d≫r, we can simplify this to:
r≈d
- The magnetic field has both vertical and horizontal components. The vertical components from opposite sides of the coil will cancel each other out, leaving only the horizontal component.
- The horizontal component of the magnetic field dBh can be expressed as:
dBh=dB⋅cos(θ)
- Using the small angle approximation, where θ is the angle between the radius of the coil and the line connecting the current element to point P, we can express cos(θ) in terms of r/d.
- To find the total magnetic field B at point P, we need to integrate dBh over the entire coil:
B=∫dBh=∫μ0Idl⋅cos(θ)4πd2
- The total length of the coil is 2πr, and we can substitute dl with rdθ to perform the integration.
- The magnetic moment μ of the coil is defined as:
μ=I⋅A=I⋅πr2
- We can express I in terms of μ:
I=μπr2
- Substituting I back into the expression for B and simplifying gives:
B=μ0μ2πd3
- This is the magnetic field at point P, where d is much larger than the radius of the coil.
The magnetic field at point P is given by:
B=μ0μ2πd3
Similar Questions
A neutral point is obtained at the centre of a vertical circular coil carrying current. The angle between the plane of the coil and the magnetic meridian is
View SolutionMagnetic fields at two points on the axis of a circular coil at a distance of 0.05m and 0.2m from the centre are in the ratio 8:1. The radius of the coil is
View Solution
Knowledge Check
A 200 turn closely wound circular coil of radius 15 cm carries a current of 4 A. The magnetic moment of this coil is
A36.5Am2B56.5Am2C66.5Am2D108Am2
The ratio of the magnetic field at the centre of a current carrying coil of the radius a and at distance 'a' from centre of the coil and perpendicular to the axis of coil is
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
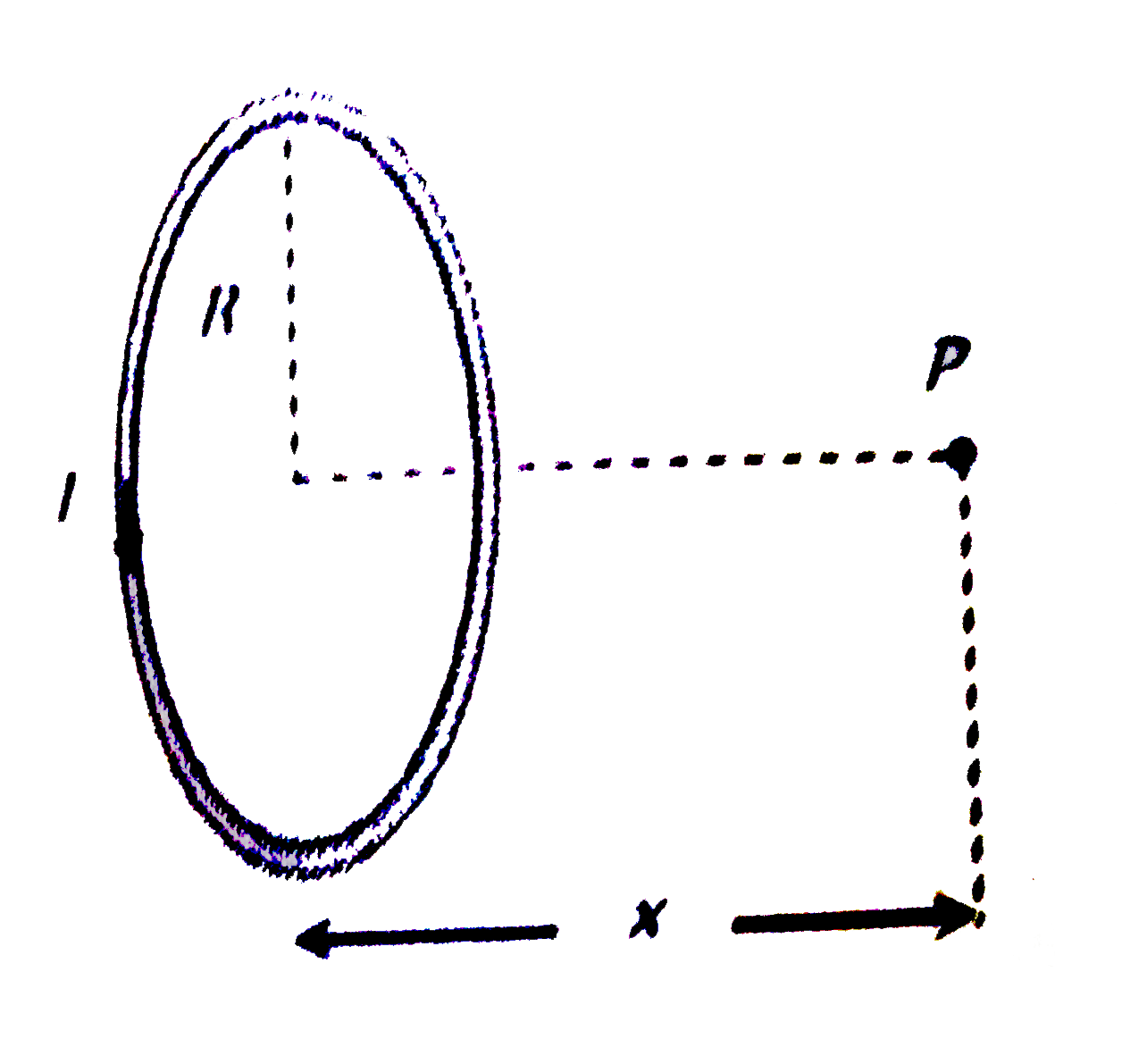
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionThe magnetic induction at the centre of a current carrying circular coil of radius 10cm is 5√5 times the magnetic induction at a point on its axis. The distance of the point from the centre of the soild in cm is
View SolutionThe magnetic field at a distance X from the centre, on the axis of a circular coil of radius R is 127 th of that at the center. The value of X is
View Solution
