A very light, rectangular wire-frame of dimensions 7cm×5cm hangs just above the free surface of a liquid of surface tension T, with its plane parallel to the free surface. The wire -frame is just brought in contact with the liquid surface and then, lifted up. If the force required to lift the wire-frame is 3.36 N, then what is the value of T in (Nm−1)?
The correct Answer is:7
To solve the problem, we need to determine the surface tension T of the liquid based on the force required to lift the wire-frame.
1. Identify the dimensions of the wire-frame:
The dimensions of the wire-frame are given as 7cm×5cm.
2. Calculate the perimeter of the wire-frame:
The perimeter P of a rectangle is calculated using the formula:
P=2×(length+width)
Substituting the dimensions:
P=2×(7cm+5cm)=2×12cm=24cm
Converting this to meters:
P=24cm=0.24m
3. Understand the force due to surface tension:
When the wire-frame is lifted, the force F required to lift it is related to the surface tension T of the liquid. The force due to surface tension acting on the wire-frame is given by:
F=2×T×P
Here, the factor of 2 accounts for the two sides of the wire-frame that are in contact with the liquid.
4. Substitute the known values:
We know that the force F required to lift the wire-frame is 3.36N. Substituting the values into the equation:
3.36=2×T×0.24
5. Solve for T:
Rearranging the equation to solve for T:
T=3.362×0.24
Simplifying the denominator:
T=3.360.48
Performing the division:
T=7N/m
Final Answer:
The value of the surface tension T is 7N/m.
---
The dimensions of the wire-frame are given as 7cm×5cm.
The perimeter P of a rectangle is calculated using the formula:
P=2×(length+width)
Substituting the dimensions:
P=2×(7cm+5cm)=2×12cm=24cm
Converting this to meters:
P=24cm=0.24m
When the wire-frame is lifted, the force F required to lift it is related to the surface tension T of the liquid. The force due to surface tension acting on the wire-frame is given by:
F=2×T×P
Here, the factor of 2 accounts for the two sides of the wire-frame that are in contact with the liquid.
We know that the force F required to lift the wire-frame is 3.36N. Substituting the values into the equation:
3.36=2×T×0.24
Rearranging the equation to solve for T:
T=3.362×0.24
Simplifying the denominator:
T=3.360.48
Performing the division:
T=7N/m
The value of the surface tension T is 7N/m.
Similar Questions
A square wire frame of side / is floating on the surface of liquid of surface tension T. The force required to pull out the frame from the liquid is
View SolutionA rectangular glass plate of dimensions 5 cm × 4 cm is placed flat on the surface of water. Find the downward force on the plate due to surface tension. Given surface tension of water = 0.073 N m−1
View Solution
Knowledge Check
A square wire fram of size L is dipped in a liquid. On taking out a membrane is formed. Ifthe surface tension of the liquid is T, the force acting on the frame will be
A2 T LB4 T LC8 T LD10 T L
A wire ring of diameter 0.03m is dipped in a liquid and pulled out gently. If a force of 0.1N is required to break the film, then what is the surface tension of the liquid?
View SolutionA rectangular wire frame of dimensions (0.25×2.0m) and mass 0.5 kg falls from a height 5m above a region occupied by uniform magnetic field of magnetic induction 1 T. The resistance of the wire frame is 18(Ω). Find
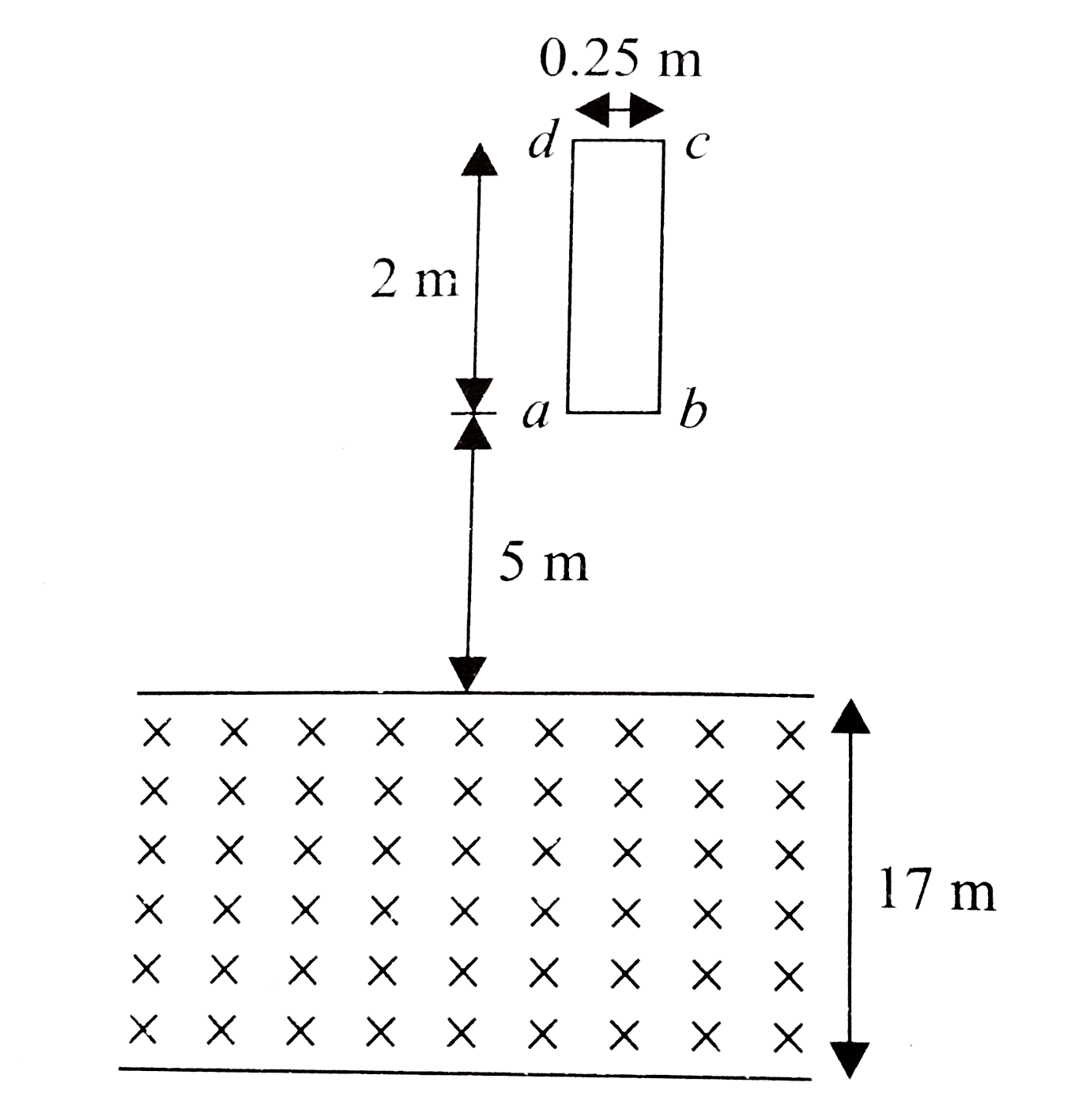
time taken to completely enter into the field is
View SolutionA square wire fram of size L is dipped in a liquid. On taking out a membrane is formed. Ifthe surface tension of the liquid is T, the force acting on the frame will be
View SolutionA rectangular wire frame of dimensions (0.25×2.0m) and mass 0.5 kg falls from a height 5m above a region occupied by uniform magnetic field of magnetic induction 1 T. The resistance of the wire frame is 18(Ω). Find
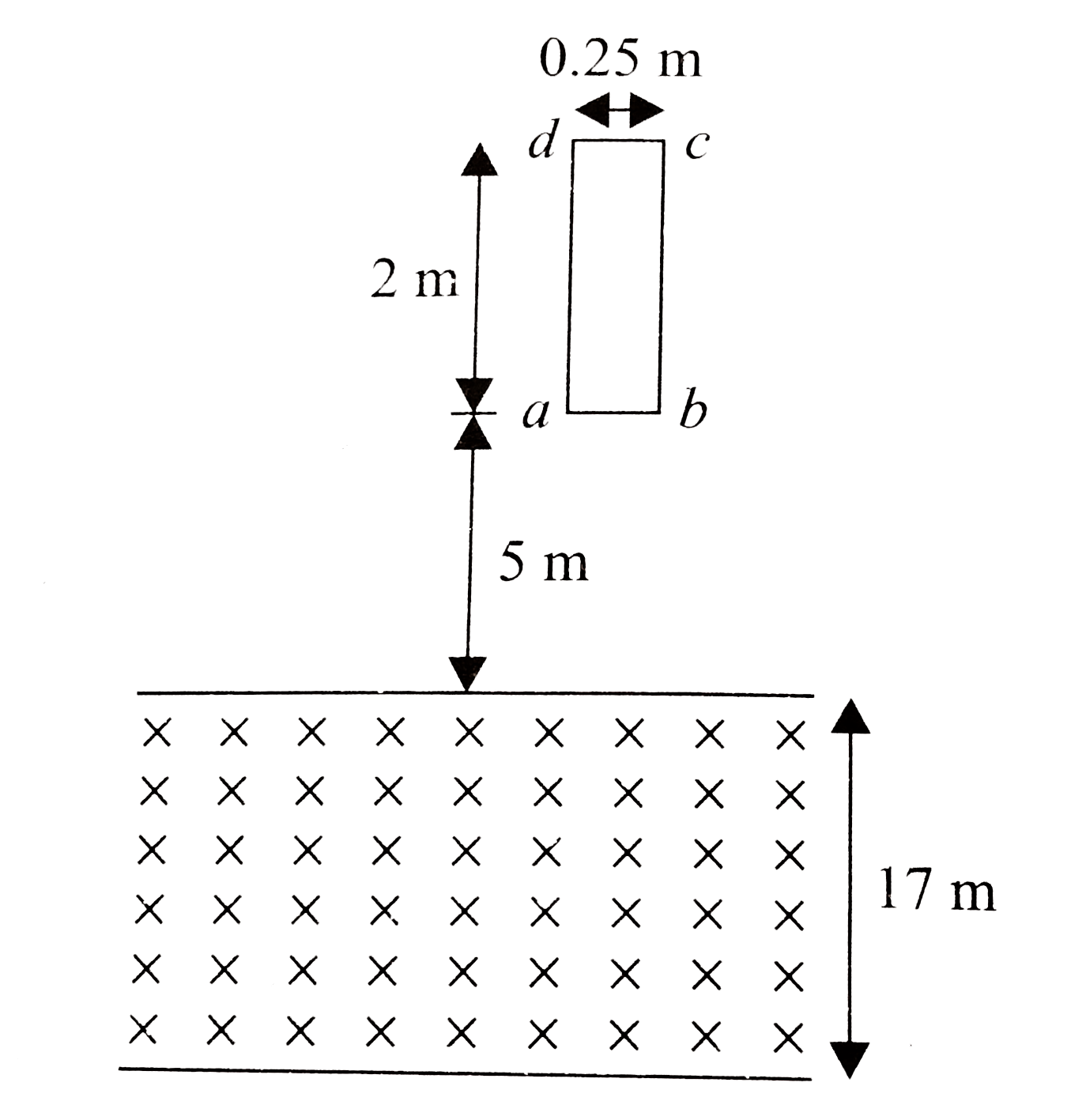
time taken by the wire frame when it just starts coming out of the magnetic field.
View SolutionThere is an air bubble of radius 1.0mm in a liquid of surface tension 0.075Nm−1 and density 103kgm−3. The bubble is at a depth of 10.0cm below the free surface of a liquid. By what amount is the pressure inside the bubble greater than the atmospheric pressure?
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
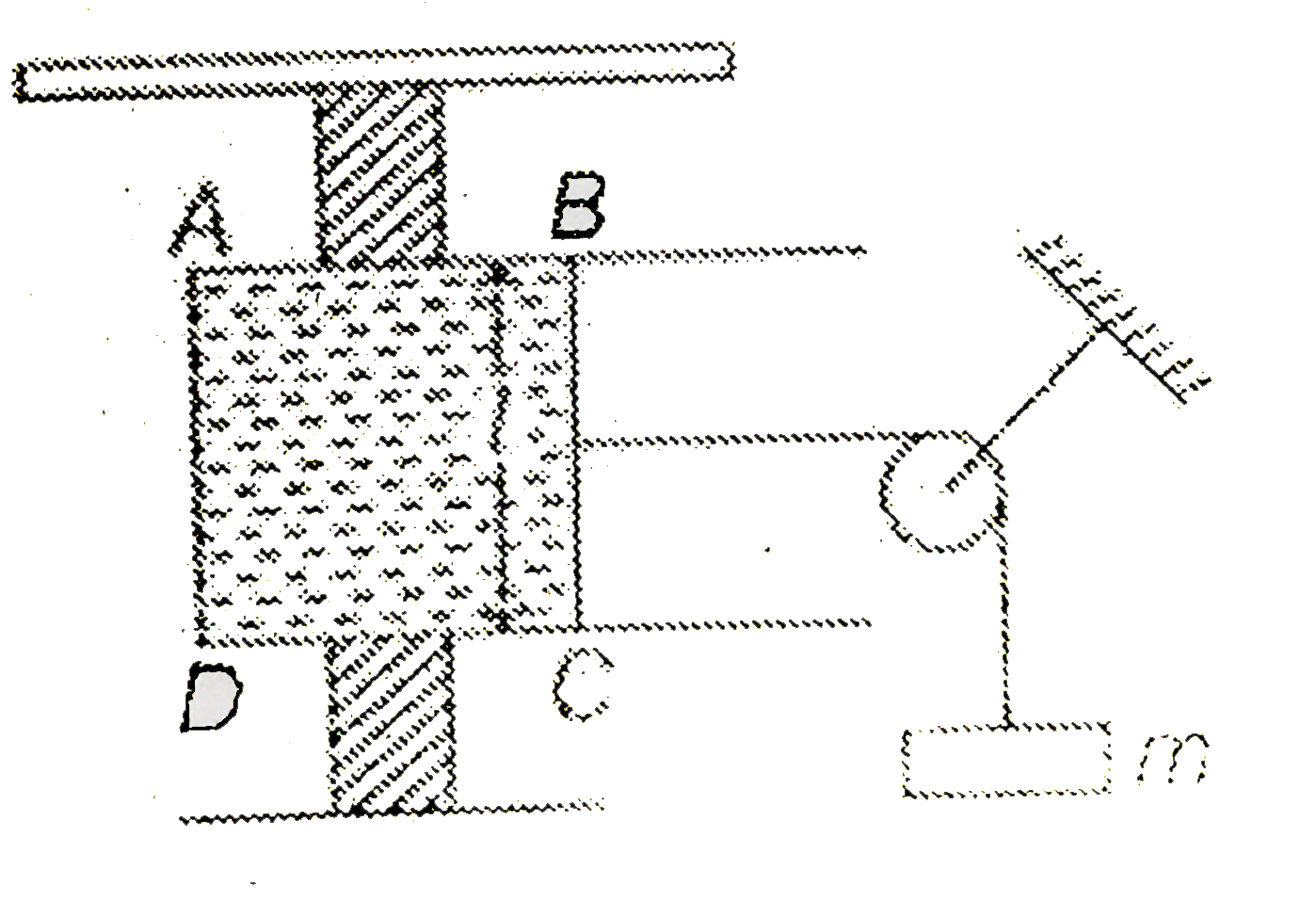
View SolutionThe length of needle foating on the surface of water is 1.5 cm the force in addition to its weight required to lift the needle from water surface will be (surface tension of water =7.5N/cm)
View Solution
