A motor generates an output power of 220 W at an angular velocity of 2100 rpm. Calculate the torque ( in Nm ) produced by the motor ? [ Take π=227]
The correct Answer is:01.00
To solve the problem of calculating the torque produced by a motor given its output power and angular velocity, we can follow these steps:
Step 1: Understand the Given Values
- Power (P) = 220 W
- Angular velocity (ω) = 2100 rpm
Step 2: Convert Angular Velocity to Radians per Second
To convert the angular velocity from revolutions per minute (rpm) to radians per second (rad/s), we use the conversion factor:
Angular velocity in rad/s=Angular velocity in rpm×2π rad1 rev×1 min60 s
Substituting the given value:
ω=2100×2×22760
Calculating this gives:
ω=2100×44420=2100×19.545≈70×227 rad/s
Thus,
ω≈70×227 rad/s
Step 3: Use the Power-Torque Relationship
The relationship between power (P), torque (τ), and angular velocity (ω) is given by:
P=τ⋅ω
From this, we can express torque as:
τ=Pω
Step 4: Substitute the Values
Substituting the values we have:
τ=220 W70×227 rad/s
Step 5: Simplify the Expression
Now, simplifying the expression:
τ=22070×227=220×770×22
The 70 and 220 can be simplified:
=31.4285722≈1 Nm
Final Answer
Thus, the torque produced by the motor is approximately:
τ≈1 Nm
- Power (P) = 220 W
- Angular velocity (ω) = 2100 rpm
To convert the angular velocity from revolutions per minute (rpm) to radians per second (rad/s), we use the conversion factor:
Angular velocity in rad/s=Angular velocity in rpm×2π rad1 rev×1 min60 s
Substituting the given value:
ω=2100×2×22760
Calculating this gives:
ω=2100×44420=2100×19.545≈70×227 rad/s
Thus,
ω≈70×227 rad/s
The relationship between power (P), torque (τ), and angular velocity (ω) is given by:
P=τ⋅ω
From this, we can express torque as:
τ=Pω
Substituting the values we have:
τ=220 W70×227 rad/s
Now, simplifying the expression:
τ=22070×227=220×770×22
The 70 and 220 can be simplified:
=31.4285722≈1 Nm
Thus, the torque produced by the motor is approximately:
τ≈1 Nm
Similar Questions
A motor is rotating at a constant angular velocity of 500 rpm. The angular displacement per second is
View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionCalculate the instantaneous power of a body rotating with angular velocity of 20rad/s−1, when an external torque of 5Nm is applied to it.
Hint : P=τω.View SolutionCalculate the instantaneous power of a body rotating with angular velocity of 20rad/s−2, when an external torque of 5Nm is applied to it.
Hint : P=τω.View SolutionThe motor of an engine is rotating about its axis with an angular velocity of 100 rpm. It comes to rest in 15 s after being switched off. Assuming constant angular deceleration, calculate the number of revolution made by it before coming to rest.
View SolutionThe motor of an engine is rotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assuming constant angular deceleration, calculate the number of revolutions made by it before coming to rest.
View SolutionAn Ac voltage is represented by e=220 sin (100π) t volt and is applied over a resistance of 110 ohm. Calculate the heat produced in 7 min.
View SolutionIn the figure given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take π=227)
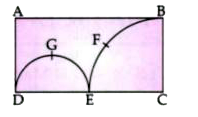 View Solution
View SolutionWhen a motor cyclist takes a U-turn in 4s what is the average angular velocity of the motor cyclist?
View Solution

