A steel scale is to be prepared such that the millimeter intervals are to be accurate within 6×10−5mm. The maximum temperature variation form the temperature of calibration during the reading of the millimeter marks is (α=12×10−6/∘C)
4.0∘C
4.5∘C
5.0∘C
5.5∘C.
To solve the problem, we need to determine the maximum temperature variation (Δθ) from the calibration temperature that will ensure the accuracy of the millimeter intervals on the steel scale.
1. Understand the given parameters:
- The accuracy of the millimeter intervals is given as ΔL=6×10−5mm.
- The coefficient of linear expansion for steel is given as α=12×10−6°C−1.
- We need to find the maximum temperature variation Δθ.
2. Use the formula for linear expansion:
The change in length (ΔL) due to a change in temperature (Δθ) is given by:
ΔL=L⋅α⋅Δθ
where L is the original length. For our case, we can take L=1mm (since we are looking at intervals of 1 mm).
3. Rearranging the formula:
We can rearrange the formula to solve for Δθ:
Δθ=ΔLL⋅α
4. Substituting the values:
Substitute ΔL=6×10−5mm, L=1mm, and α=12×10−6°C−1:
Δθ=6×10−5mm1mm⋅12×10−6°C−1
5. Calculating the value:
Δθ=6×10−512×10−6=612×101=0.5×101=5°C
6. Final Answer:
The maximum temperature variation from the calibration temperature is Δθ=5°C.
- The accuracy of the millimeter intervals is given as ΔL=6×10−5mm.
- The coefficient of linear expansion for steel is given as α=12×10−6°C−1.
- We need to find the maximum temperature variation Δθ.
The change in length (ΔL) due to a change in temperature (Δθ) is given by:
ΔL=L⋅α⋅Δθ
where L is the original length. For our case, we can take L=1mm (since we are looking at intervals of 1 mm).
We can rearrange the formula to solve for Δθ:
Δθ=ΔLL⋅α
Substitute ΔL=6×10−5mm, L=1mm, and α=12×10−6°C−1:
Δθ=6×10−5mm1mm⋅12×10−6°C−1
Δθ=6×10−512×10−6=612×101=0.5×101=5°C
The maximum temperature variation from the calibration temperature is Δθ=5°C.
Similar Questions
A steel tape measures that length of a copper rod as 90.0 cm when both are at 10∘C, the calibration temperature, for the tape. What would the tape read for the length of the rod when both are at 30∘C. Given αsteel=1.2×10−5 per.∘CandαCu=1.7×10−5per.∘C
View SolutionWhat is the percentage change in length of 1m iron rod it its temperature changes by 100∘C.α for iron is 2×10−5/∘C.
View Solution
Knowledge Check
A steel metre scale is to be ruled so that the millimetre intervals are accurate to within about 5×10−5mm at a certain temperature. What is the maximum temperature variation allowable during the ruling ? Given α for steel =1.1×10−5.∘C−1.
A8∘CB9∘CC4.5∘CD10∘C
Two stars radiate maximum energy at wavelength 3.6×10−7 m and 4.8×10−7 m respectively. What is the ratio of their temperatures ?
View SolutionThe scale on a steel meter stick is calibrated at 15∘C. What is the error in the reading of 60cm at 27∘C ? αsteel=1.2×10−5(.∘C)−1.
View SolutionA steel tape is correctly calibrated at 20∘C and is used to measure the length of a table at 30∘C. Find the percentage error in the measurement of length. [αsteel=11×10−5/.∘C]
View SolutionThe temperature of sun is 5500 K and it emits maximum intensity radiation in the yellow region(5.5×10−7m). The maximum radiation from a furnace occurs at wavelength 11×10−7m The temperature of furnace is
View SolutionA steel tape placed around the earth at the equator when the temperature is 10∘C. What will be the clearance between the tape and the ground (assumed to be uniform) if the temperature of the tape rises to 40∘C? Neglect expansion of the earth. Radius of earth at equator is 6400km & αsteel=1.2×10−5K−1
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends
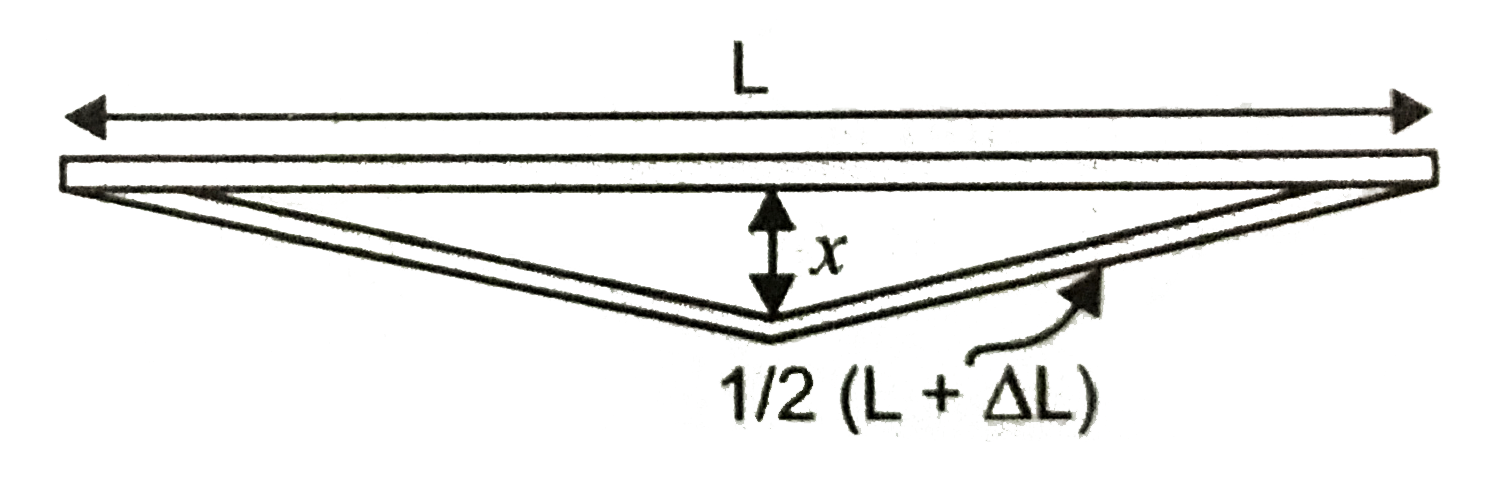
on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be? ( alpha_(A)=3x10^(-6)/ C )
View Solution