Positive charge q is given to each plate of a parallel plate air capacitor having area of each plate A and seperation between them, d. Then find
(i) Capacitance of the system. (ii) Charges appearing on each surface of plates
(iii) Electric field between the plates (iv) Potential diffrence between the plates
(v) Energy stored between hte plates
since both the plates are identically charged, therefore, capacitance becomes equal to zero
energy stored in the space between the capacitor plates is equal to q2ε0A2.
no charge appears on inner surface of the plates
potential difference between the plates is equal to 2qdε0A
The correct Answer is:C
To solve the problem step by step, we will find the required parameters for the parallel plate capacitor with the given conditions.
Step 1: Find the Capacitance of the System
The formula for the capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
where:
- ε0 is the permittivity of free space (approximately 8.85×10−12F/m),
- A is the area of each plate,
- d is the separation between the plates.
Step 2: Charges Appearing on Each Surface of Plates
Since a positive charge Q is given to each plate, the charges on the plates will distribute as follows:
- The outer surfaces of both plates will have a charge of +Q.
- The inner surfaces of both plates will have a charge of 0 because the charges are static and there is no movement of charge within the capacitor.
Step 3: Electric Field Between the Plates
The electric field E between the plates of a parallel plate capacitor is given by:
E=σε0
where σ is the surface charge density given by:
σ=QA
Thus, substituting σ into the electric field equation:
E=QAε0
Step 4: Potential Difference Between the Plates
The potential difference V between the plates is given by:
V=E⋅d
Substituting the expression for E:
V=(QAε0)⋅d=QdAε0
Step 5: Energy Stored Between the Plates
The energy U stored in the capacitor is given by:
U=12CV
Substituting the expressions for C and V:
U=12(ε0Ad)(QdAε0)=12Q2ε0A
Summary of Results
1. Capacitance: C=ε0Ad
2. Charges on Plates: Outer surfaces: +Q; Inner surfaces: 0
3. Electric Field: E=QAε0
4. Potential Difference: V=QdAε0
5. Energy Stored: U=12Q2ε0A
The formula for the capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
where:
- ε0 is the permittivity of free space (approximately 8.85×10−12F/m),
- A is the area of each plate,
- d is the separation between the plates.
Since a positive charge Q is given to each plate, the charges on the plates will distribute as follows:
- The outer surfaces of both plates will have a charge of +Q.
- The inner surfaces of both plates will have a charge of 0 because the charges are static and there is no movement of charge within the capacitor.
The electric field E between the plates of a parallel plate capacitor is given by:
E=σε0
where σ is the surface charge density given by:
σ=QA
Thus, substituting σ into the electric field equation:
E=QAε0
The potential difference V between the plates is given by:
V=E⋅d
Substituting the expression for E:
V=(QAε0)⋅d=QdAε0
The energy U stored in the capacitor is given by:
U=12CV
Substituting the expressions for C and V:
U=12(ε0Ad)(QdAε0)=12Q2ε0A
1. Capacitance: C=ε0Ad
2. Charges on Plates: Outer surfaces: +Q; Inner surfaces: 0
3. Electric Field: E=QAε0
4. Potential Difference: V=QdAε0
5. Energy Stored: U=12Q2ε0A
Similar Questions
Knowledge Check
- Question 1 - Select One
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
What is the area of the plates of a 2 farad parallel plate air capacitor, given that the separation between the plates is 0.5 cm?
View SolutionWhat is the area of the plates of a 2 farad parallel plate air capacitor, given that the separation between the plates is 0.5 cm?
View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
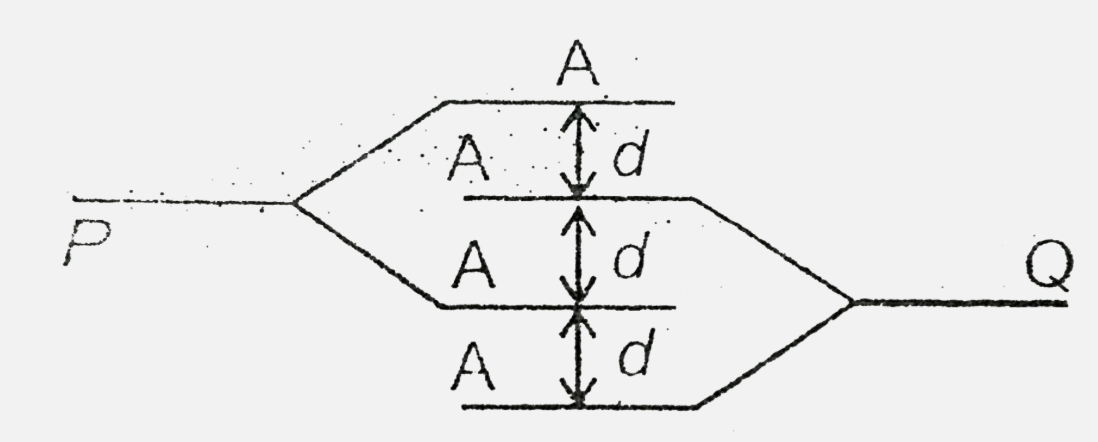
View SolutionFind the charge on each plate given area of each plate is A and separation between two consecutive plates is d.
 View Solution
View SolutionIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius r with direction T. On what power of r, will the square of time period depends if the gravitational force of attraction between the planet and the star is proportional to r−5/2 .
View SolutionFind the equivalent capacitance between A and B.A: area of each plate, d: separation between the plates.
 View Solution
View Solution