For a particle of a rotating rigid body, , which of the following are correct ?
is independent of r
The correct Answer is:D
To solve the question regarding the relationship v=rω for a particle of a rotating rigid body, we can break it down into a step-by-step analysis.
1. Understanding the Equation: The equation v=rω relates the linear velocity v of a particle to its distance r from the axis of rotation and the angular velocity ω. Here, v is the linear speed, r is the radius (or distance from the axis of rotation), and ω is the angular velocity.
2. Proportionality: From the equation, we can see that the linear velocity v is directly proportional to the radius r when ω is constant. This means that if the radius increases, the linear velocity also increases, assuming that the angular velocity remains the same.
3. Constant Angular Velocity: In a rigid body rotating about a fixed axis, the angular velocity ω is constant for all points in the body. This means that every particle in the rigid body rotates with the same angular speed, regardless of its distance from the axis of rotation.
4. Independence of Radius: Since ω is constant for a rigid body, it is independent of the radius r. This means that changes in the radius do not affect the angular velocity.
5. Conclusion: Based on the analysis, we can conclude that the correct statement regarding the relationship v=rω is that ω is independent of the radius r.
Final Answer:
The correct statement is that ω is independent of the radius r.
The correct statement is that ω is independent of the radius r.
Similar Questions
Which of the following is correct w.r.t. Lamarckism?
View SolutionIf the velocity of the particle is given by v=√x and initially particle was at x=4m then which of the following are correct.
View SolutionA particle is confined to rotate in a circular path decreasing linear speed, then which of the following is correct?
View SolutionIf a=−ω2x represents the acceleration of a particle executing S.H.M.which of the following statement(s) is /are correct ?
View SolutionThe variation of angular position θ, of a point on a rotating rigid body, with time t is shown in Fig. Is the body rotating clock wise or anti-clockwise ?
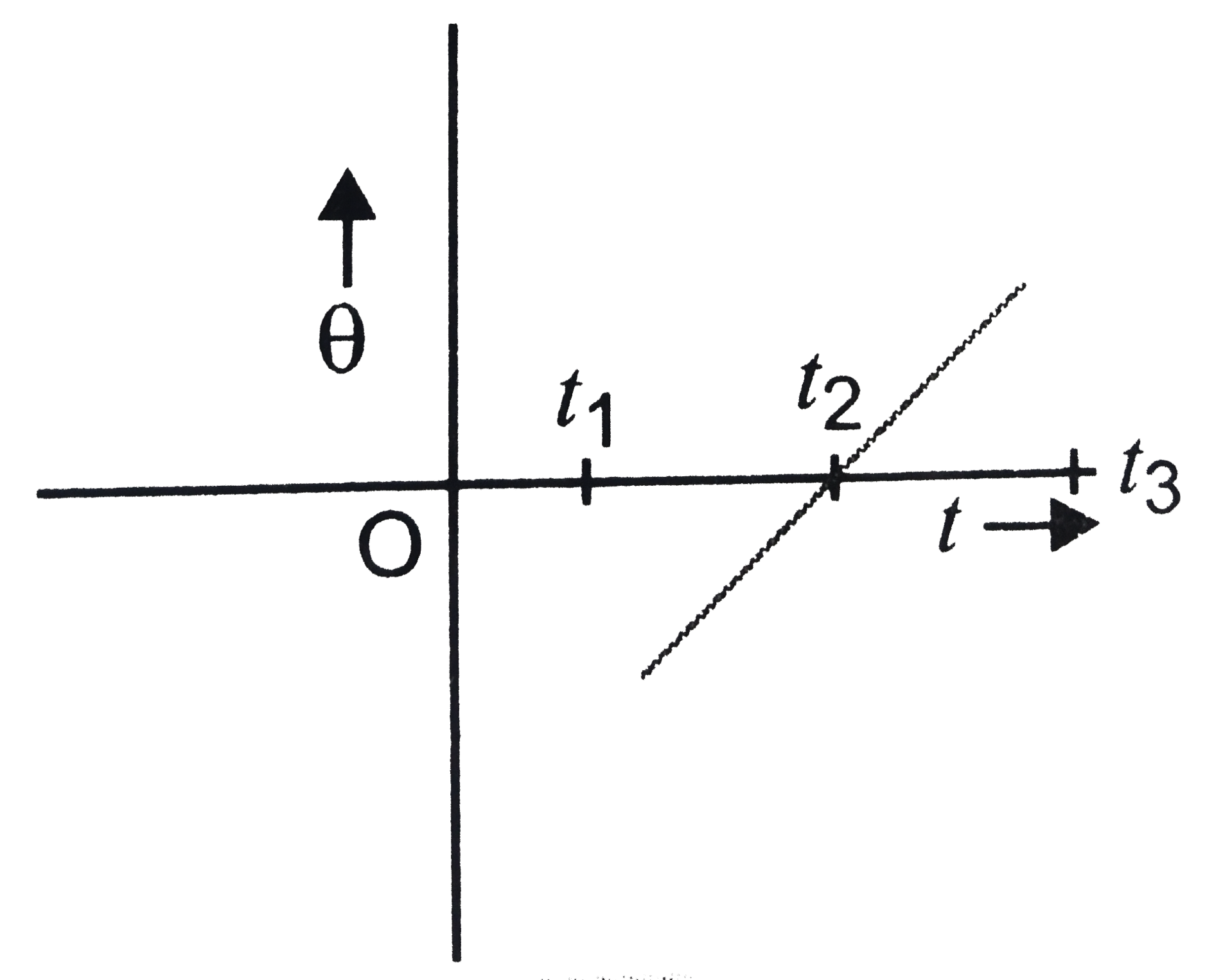
View SolutionLet T represent the true weight of a body, B the force of buoyancy on the body when immersed in a liquid. A represents the apparent weight of the body and W be twice the weight of liquid displaced by te body. Then which of the following relation is correct?
View Solutionthe variaton of angular postion θ of a point on a rotating rigid body with time t is shown in figure Is the body rotating clokwise or anti- clokwise ?
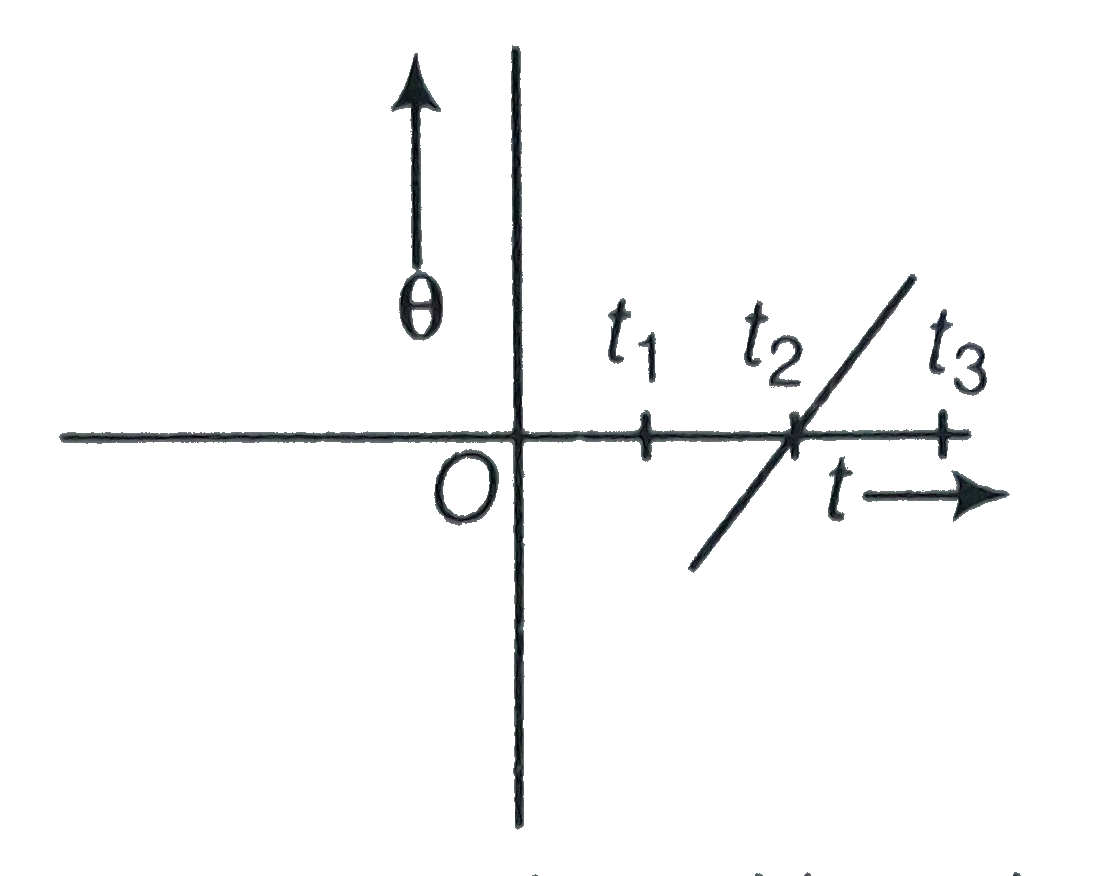
View SolutionA particle moves so that its position vector is given by →r=cosωtˆx+sinωtˆy, where ω is a constant which of the following is true ?
View SolutionA particle moves so that its position vector is given by →r=cosωtˆx+sinωtˆy, where ω is a constant which of the following is true ?
View SolutionWhich one of the following statements is correct?
View Solution