If a stone is to hit at a point which is at a horizontal distance 100 m away and at a hight 50 m above the point from where the stone starts, then what is the value of initial speed u if the stone is launched at an angle 45∘?
10√2m/s
10√5m/s
20√5m/s
20√10m/s
The correct Answer is:C
To solve the problem of finding the initial speed u required for a stone to hit a target at a horizontal distance of 100 m and a height of 50 m when launched at an angle of 45∘, we can follow these steps:
Step 1: Define the known variables
- Horizontal distance (x): 100 m
- Height (y): 50 m
- Launch angle (θ): 45∘
- Acceleration due to gravity (g): approximately 10m/s2
Step 2: Break down the initial velocity into components
The initial velocity u can be broken down into horizontal and vertical components:
- Horizontal component (ux):
ux=ucosθ
- Vertical component (uy):
uy=usinθ
Since θ=45∘, we have:
cos45∘=sin45∘=1√2
Thus,
ux=u⋅1√2,uy=u⋅1√2
Step 3: Find the time of flight
The horizontal distance covered is given by:
x=ux⋅t⟹t=xux=100u⋅1√2=100√2u
Step 4: Use the vertical motion equation
The vertical motion can be described by the equation:
y=uy⋅t−12gt2
Substituting for y, uy, and t:
50=u⋅1√2⋅(100√2u)−12g(100√2u)2
Step 5: Simplify the equation
Substituting g=10m/s2:
50=100−12⋅10⋅(100√2u)2
50=100−5⋅20000u2
50=100−100000u2
100000u2=50
u2=10000050=2000
u=√2000=44.72m/s
Final Answer
The initial speed u required for the stone to hit the target is approximately 44.72m/s.
- Horizontal distance (x): 100 m
- Height (y): 50 m
- Launch angle (θ): 45∘
- Acceleration due to gravity (g): approximately 10m/s2
The initial velocity u can be broken down into horizontal and vertical components:
- Horizontal component (ux):
ux=ucosθ
- Vertical component (uy):
uy=usinθ
cos45∘=sin45∘=1√2
Thus,
ux=u⋅1√2,uy=u⋅1√2
The horizontal distance covered is given by:
x=ux⋅t⟹t=xux=100u⋅1√2=100√2u
The vertical motion can be described by the equation:
y=uy⋅t−12gt2
Substituting for y, uy, and t:
50=u⋅1√2⋅(100√2u)−12g(100√2u)2
Substituting g=10m/s2:
50=100−12⋅10⋅(100√2u)2
50=100−5⋅20000u2
50=100−100000u2
100000u2=50
u2=10000050=2000
u=√2000=44.72m/s
The initial speed u required for the stone to hit the target is approximately 44.72m/s.
Similar Questions
If a stone is to hit at a point which is at a distance d away and at a height h (Fig. 5.200) above the point from where the stone starts, then what is the value of initial speed u if the stone is launched at an angle θ ?
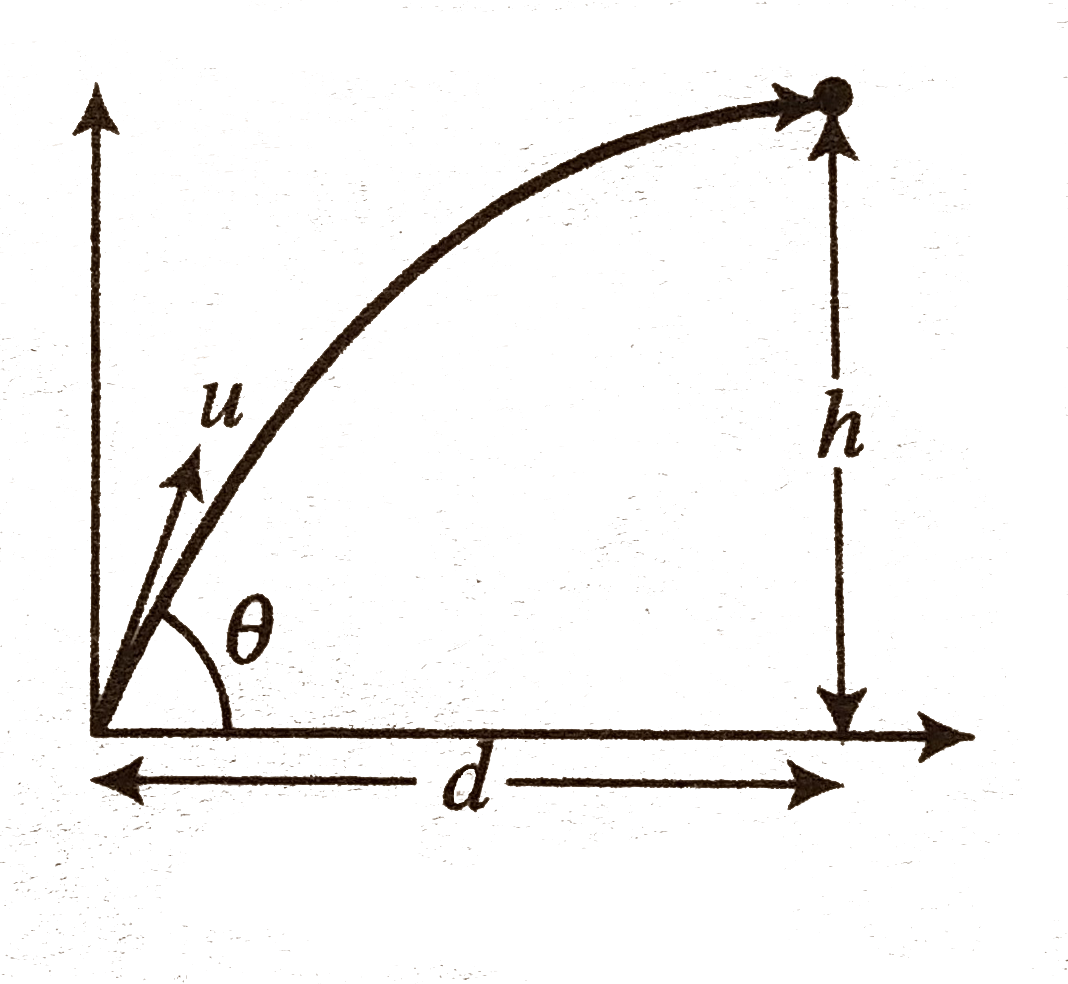 .
.
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is dropped from a rising balloon at a height of 76 m above the ground and reaches the ground in 6s. What was the velocity of the balloon when the stone was dropped?
View SolutionA stone tied to the end of string 1m long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revolution in 44s, What is the magnitude and direction of acceleration of the ston is ?
View SolutionA boy whirls a stone of small mass in a horizontal circle of radius 1.5m and at height 2.9m above level ground. The string breacks and the stone flies off horizontally and strikes the ground after travelling a horizontal distance of 10m . What is the magnitude of the centripetal acceleration of the stone while in circular motion ?
View SolutionA stone is thrown at an angle of 45∘ to the horizontal with kinetic energy K. The kinetic energy at the highest point is
View SolutionThe sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source ?
View SolutionA stone is thrown horizontally with velocity g ms−1 from the top of a tower of height g metre. The velocity with which it hits the ground is (in ms−1)
View SolutionA boy whirls a stone of small mass in a horizontal circle of radius 1.5m and at height 2.9m above level ground. The string breaks and the stone flies off horizontally and strikes the ground after travelling a horizontal distance of 10m . What is the magnitude of the centripetal acceleration of the stone while in circular motion ?
View Solution
