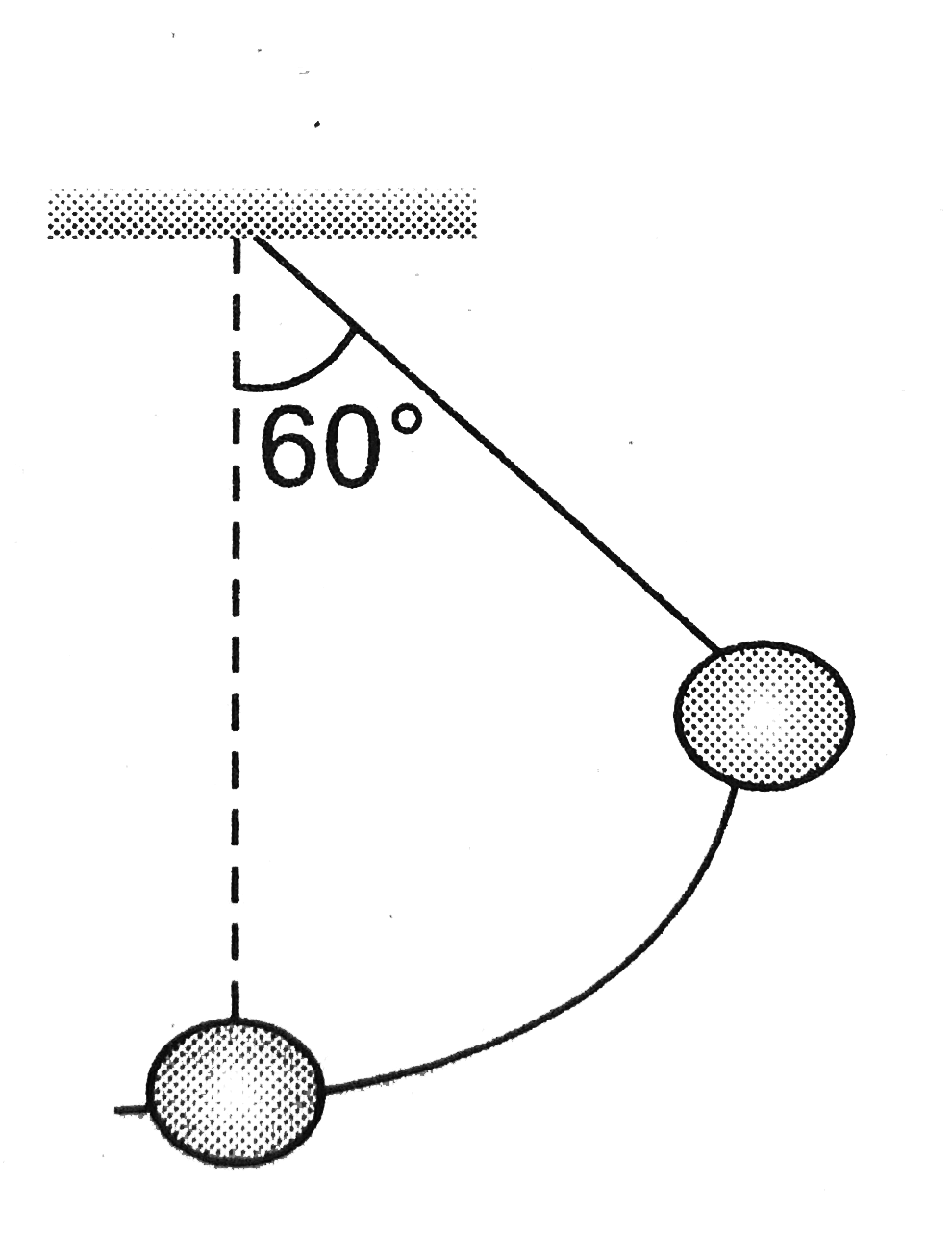
A bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
√gl
√3gl
√2gl
√5gl
The correct Answer is:A
To solve the problem of finding the speed of the bob at the lowest position when it is released from an angle of 60 degrees with the vertical, we can use the principle of conservation of mechanical energy. Here’s a step-by-step solution:
Step 1: Identify the initial and final positions
- The bob is initially at point A, making an angle of 60 degrees with the vertical.
- The lowest position is point B, where the bob is directly below the point of suspension.
Step 2: Determine the height difference
- The length of the string is L.
- At point A, the height hA can be calculated using trigonometry. The vertical component of the string length when the bob is at 60 degrees is given by:
OC=Lcos(60∘)=L⋅12=L2
- Therefore, the height hA from the lowest point B to point A is:
hA=L−OC=L−L2=L2
Step 3: Apply the conservation of energy
- The total mechanical energy at point A (initial position) is equal to the total mechanical energy at point B (lowest position).
- At point A, the kinetic energy KEA=0 (since it is released from rest) and the potential energy PEA=mghA.
- At point B, the potential energy PEB=0 (as it is at the lowest point) and the kinetic energy KEB=12mv2B.
Step 4: Set up the energy conservation equation
KEA+PEA=KEB+PEB
Substituting the values:
0+mg(L2)=12mv2B+0
Step 5: Simplify the equation
- Cancel m from both sides (assuming m≠0):
g(L2)=12v2B
- Rearranging gives:
v2B=gL
Step 6: Solve for vB
Taking the square root:
vB=√gL
Conclusion
The speed of the bob at the lowest position is:
vB=√gL
- The bob is initially at point A, making an angle of 60 degrees with the vertical.
- The lowest position is point B, where the bob is directly below the point of suspension.
- The length of the string is L.
- At point A, the height hA can be calculated using trigonometry. The vertical component of the string length when the bob is at 60 degrees is given by:
OC=Lcos(60∘)=L⋅12=L2
- Therefore, the height hA from the lowest point B to point A is:
hA=L−OC=L−L2=L2
- The total mechanical energy at point A (initial position) is equal to the total mechanical energy at point B (lowest position).
- At point A, the kinetic energy KEA=0 (since it is released from rest) and the potential energy PEA=mghA.
- At point B, the potential energy PEB=0 (as it is at the lowest point) and the kinetic energy KEB=12mv2B.
KEA+PEA=KEB+PEB
Substituting the values:
0+mg(L2)=12mv2B+0
- Cancel m from both sides (assuming m≠0):
g(L2)=12v2B
- Rearranging gives:
v2B=gL
Taking the square root:
vB=√gL
The speed of the bob at the lowest position is:
vB=√gL
Similar Questions
A bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Upto what maximum height will the bob rise with respect to the bottommost point ?
View SolutionA bob hangs from a rigid support by an inextensible string of length l. If it is displaced through a distance l (from the lowest position) keeping the string straight and then released. The speed of the bob at the lowest position is

View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionA body is hanging from a rigid support. by an inextensible string of length '1' . It is struck inelastically by an identical body of mass in with horizontal velocity v=√2gl the tension in the string increases just after the striking by
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View SolutionA ball of mass 1kg is suspended by an inextensible string 1m long attached to a point O of a smooth horizontal bar resting on fixed smooth supports A and B. The ball is released from rest from the position when the string makes an angle 30∘ with the vertical. The mass of the bar is 4kg. The displacement of bar when ball reaches the other extreme position (in m) is

View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View Solution
