A pulley fixed to the ceiling carries a string with blocks of mass and attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
(a)g
(b)
(c)
(d)zero
The correct Answer is:C
To find the acceleration of the center of mass of the system consisting of two blocks of mass m and 3m connected by a string over a pulley, we can follow these steps:
Step 1: Identify the Forces Acting on Each Mass
- The block of mass m experiences a downward force due to gravity, which is mg.
- The block of mass 3m experiences a downward force due to gravity, which is 3mg.
Step 2: Determine the Net Force Acting on the System
- The net force acting on the system can be calculated by considering the difference in the gravitational forces acting on the two blocks:
\(
F_{\text{net}} = F_{3m} - F_{m} = 3mg - mg = 2mg
\)
Step 3: Calculate the Total Mass of the System
- The total mass of the system is the sum of the masses of the two blocks:
\(
M_{\text{total}} = m + 3m = 4m
\)
Step 4: Apply Newton's Second Law to Find the Acceleration
- According to Newton's second law, the acceleration a of the system can be found using the formula:
\(
F_{\text{net}} = M_{\text{total}} \cdot a
\)
Substituting the values we found:
\(
2mg = 4m \cdot a
\)
Dividing both sides by 4m gives:
\(
a = \frac{2mg}{4m} = \frac{2g}{4} = \frac{g}{2}
\)
Step 5: Determine the Direction of the Acceleration
- Since the heavier block (mass 3m) is pulling the lighter block (mass m) downwards, the acceleration of the center of mass will also be directed downwards.
Step 6: Conclusion
- The acceleration of the center of mass of the system is:
\(
a_{\text{CM}} = \frac{g}{2}
\)
The negative sign indicates that the direction of acceleration is downward.
Final Answer
The acceleration of the center of mass is \( \frac{g}{2} \) downward.
---
- The block of mass m experiences a downward force due to gravity, which is mg.
- The block of mass 3m experiences a downward force due to gravity, which is 3mg.
- The net force acting on the system can be calculated by considering the difference in the gravitational forces acting on the two blocks:
\(
F_{\text{net}} = F_{3m} - F_{m} = 3mg - mg = 2mg
\)
- The total mass of the system is the sum of the masses of the two blocks:
\(
M_{\text{total}} = m + 3m = 4m
\)
- According to Newton's second law, the acceleration a of the system can be found using the formula:
\(
F_{\text{net}} = M_{\text{total}} \cdot a
\)
Substituting the values we found:
\(
2mg = 4m \cdot a
\)
Dividing both sides by 4m gives:
\(
a = \frac{2mg}{4m} = \frac{2g}{4} = \frac{g}{2}
\)
- Since the heavier block (mass 3m) is pulling the lighter block (mass m) downwards, the acceleration of the center of mass will also be directed downwards.
- The acceleration of the center of mass of the system is:
\(
a_{\text{CM}} = \frac{g}{2}
\)
The negative sign indicates that the direction of acceleration is downward.
The acceleration of the center of mass is \( \frac{g}{2} \) downward.
Similar Questions
A pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
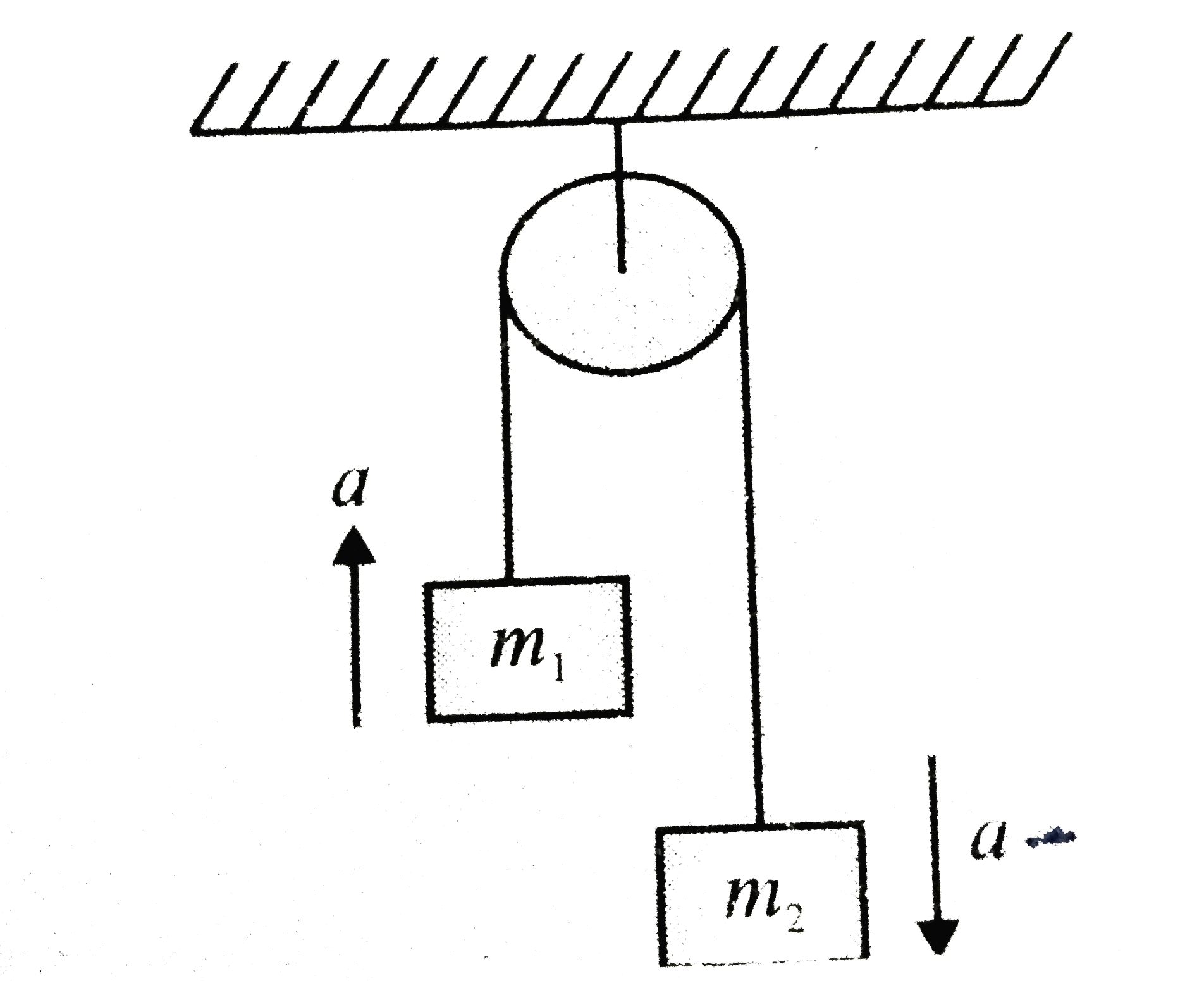
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
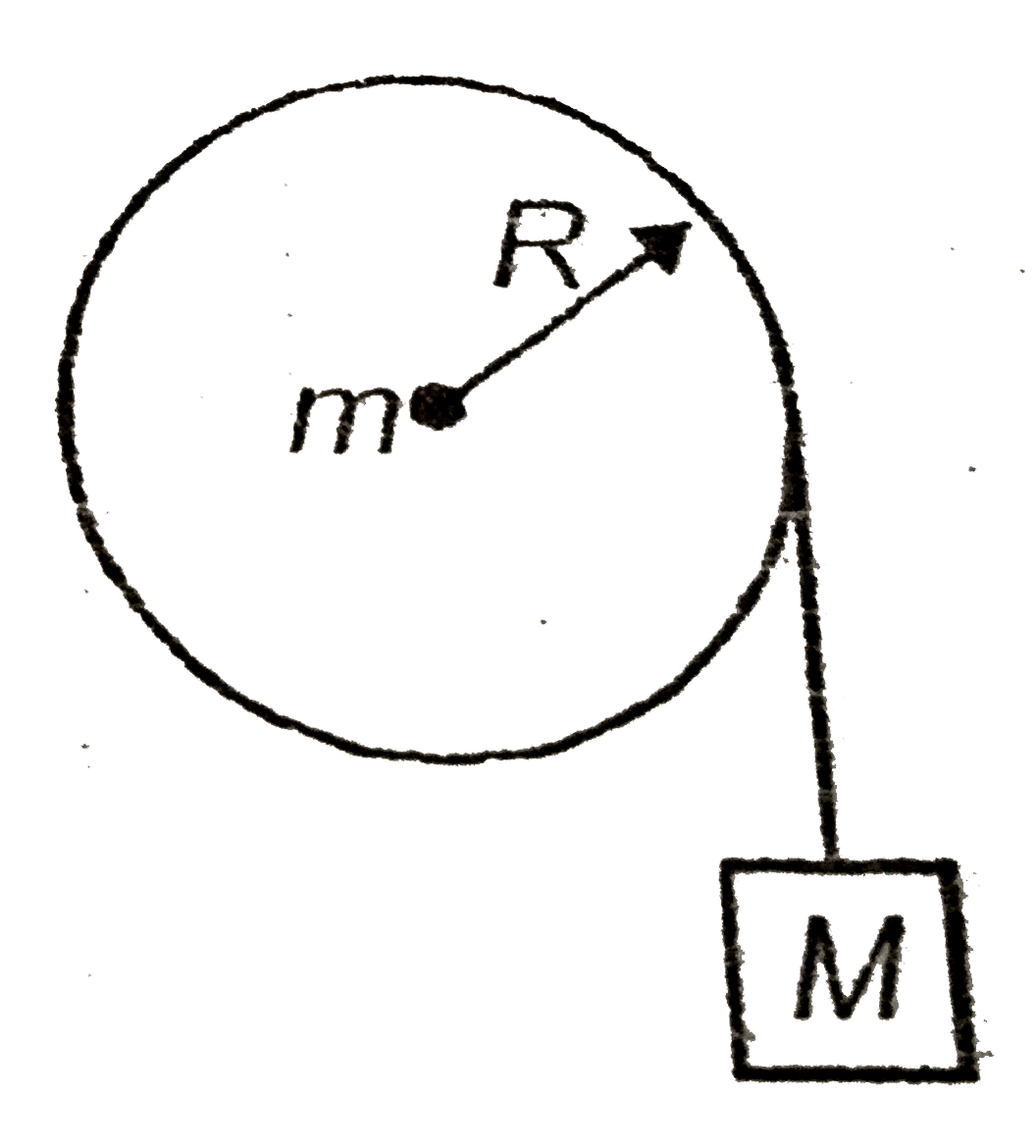
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
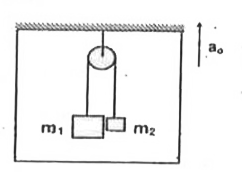
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.
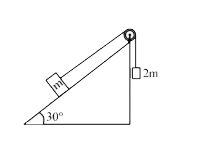
View SolutionTwo blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
View Solution
