Identify the correct trend given below:
(Atomic No = Ti:22,Cr:24 and Mo : 42)
Δof[Cr(H2O)6]2+and>[Mo(H2O)6]2+
Δof[Ti(H2O)6]3+>[Ti(H2O)6]2+
Δof[Cr(H2O)6]2+and>[Mo(H2O)6]2+
Δof[Ti(H2O)6]3+<[Ti(H2O)6]2+
Δof[Cr(H2O)6]2+and<[Mo(H2O)6]2+
Δof[Ti(H2O)6]3+>[Ti(H2O)6]2+
Δof[Cr(H2O)6]2+and<[Mo(H2O)6]2+
Δof[Ti(H2O)6]3+<[Ti(H2O)6]2+
The correct Answer is:C
To identify the correct trend in crystal field splitting energy (Δo) for the given transition metals (Titanium, Chromium, and Molybdenum), we need to consider the factors that influence Δo. These factors include the charge on the metal ion and the size of the metal ion.
1. Understanding Crystal Field Splitting Energy (Δo):
- Δo is the energy difference between the split d-orbitals in a crystal field. It is influenced by the charge of the metal ion and its size.
2. Analyzing the Metal Ions:
- The given metals are Titanium (Ti), Chromium (Cr), and Molybdenum (Mo).
- Their atomic numbers are:
- Titanium (Ti): 22
- Chromium (Cr): 24
- Molybdenum (Mo): 42
3. Comparing Sizes:
- As we move down the group in the periodic table, the atomic radius increases. Therefore, the order of size is:
- Mo > Cr > Ti
- This means that Molybdenum has the largest atomic radius, followed by Chromium, and then Titanium has the smallest.
4. Charge Consideration:
- The charge on the metal ions also affects Δo. Higher charge typically leads to a larger Δo.
- For example:
- Ti can exist in +2 and +3 oxidation states.
- Cr can exist in +2 and +3 oxidation states.
- Mo can exist in +2 and +3 oxidation states.
5. Determining Δo:
- For the same ligand (like H2O), Δo is inversely proportional to the size of the metal ion and directly proportional to the charge.
- Therefore, for the same charge:
- Δo(Cr) > Δo(Mo) because Cr is smaller than Mo.
- For Titanium:
- Δo(Ti^3+) > Δo(Ti^2+) because Ti^3+ has a higher charge than Ti^2+.
6. Final Comparison:
- Comparing all three:
- Δo(Cr^2+) > Δo(Mo^2+) (due to size)
- Δo(Ti^3+) > Δo(Ti^2+) (due to charge)
- Thus, we can summarize the trend as:
- Δo(Ti^3+) > Δo(Cr^2+) > Δo(Mo^2+) > Δo(Ti^2+)
Conclusion:
The correct trend in crystal field splitting energy (Δo) for the given transition metals is:
- Δo(Ti^3+) > Δo(Cr^2+) > Δo(Mo^2+) > Δo(Ti^2+)
- Δo is the energy difference between the split d-orbitals in a crystal field. It is influenced by the charge of the metal ion and its size.
- The given metals are Titanium (Ti), Chromium (Cr), and Molybdenum (Mo).
- Their atomic numbers are:
- Titanium (Ti): 22
- Chromium (Cr): 24
- Molybdenum (Mo): 42
- As we move down the group in the periodic table, the atomic radius increases. Therefore, the order of size is:
- Mo > Cr > Ti
- This means that Molybdenum has the largest atomic radius, followed by Chromium, and then Titanium has the smallest.
- The charge on the metal ions also affects Δo. Higher charge typically leads to a larger Δo.
- For example:
- Ti can exist in +2 and +3 oxidation states.
- Cr can exist in +2 and +3 oxidation states.
- Mo can exist in +2 and +3 oxidation states.
- For the same ligand (like H2O), Δo is inversely proportional to the size of the metal ion and directly proportional to the charge.
- Therefore, for the same charge:
- Δo(Cr) > Δo(Mo) because Cr is smaller than Mo.
- For Titanium:
- Δo(Ti^3+) > Δo(Ti^2+) because Ti^3+ has a higher charge than Ti^2+.
- Comparing all three:
- Δo(Cr^2+) > Δo(Mo^2+) (due to size)
- Δo(Ti^3+) > Δo(Ti^2+) (due to charge)
- Thus, we can summarize the trend as:
- Δo(Ti^3+) > Δo(Cr^2+) > Δo(Mo^2+) > Δo(Ti^2+)
The correct trend in crystal field splitting energy (Δo) for the given transition metals is:
- Δo(Ti^3+) > Δo(Cr^2+) > Δo(Mo^2+) > Δo(Ti^2+)
Similar Questions
Knowledge Check
Identify ‘Z' in the reaction given below:
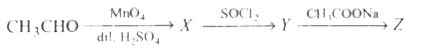 ACH3CHOB(CH3CO)2OC(CH3)2CHCH2COOHD(CH2ClCO)2O
ACH3CHOB(CH3CO)2OC(CH3)2CHCH2COOHD(CH2ClCO)2OIdentify 'Z' in the reaction given below :
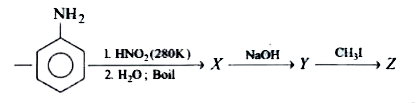 A
A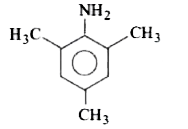 B
B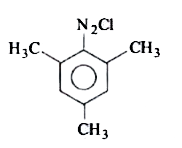 C
C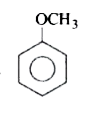 D
D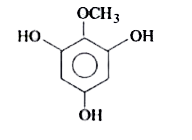
Identify the correct match from the column given below .

View SolutionIdentify 'X' in the flowchart given below.

View SolutionIdentify the incorrect statement from the given below.
View SolutionIdentify the figure given below.

View SolutionIdentify the correct description of the below figure
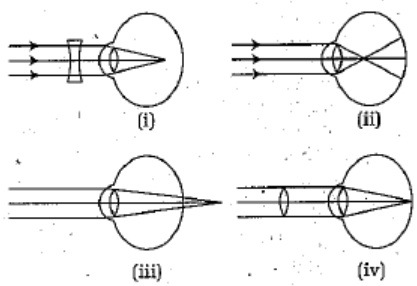
View SolutionIdentify the correct set of parts in the diagram given below.

View Solution

