Two different electrolytic cells filled with molten Cu(NO3)2 and molten Al(NO3)3 respectively are connected in series. When electricity is passed 2.7 g Al is deposited on electrode. Calculate the weight of Cu deposited on cathode.
[Cu=63.5,Al=27.0gmol−1]
190.5 g
9.525 g
63.5 g
31.75 g
The correct Answer is:B
To solve the problem, we will use Faraday's law of electrolysis, which states that the amount of substance deposited or liberated at an electrode during electrolysis is directly proportional to the quantity of electricity passed through the electrolyte.
1. Identify the Given Data:
- Weight of aluminum deposited (W_Al) = 2.7 g
- Atomic mass of copper (Cu) = 63.5 g/mol
- Atomic mass of aluminum (Al) = 27.0 g/mol
2. Calculate the Equivalent Weights:
- For Copper (Cu):
- The n-factor for Cu in Cu(NO₃)₂ is 2 (since Cu is in +2 oxidation state).
- Equivalent weight of Cu = Atomic mass of Cu / n-factor = 63.5 g/mol / 2 = 31.75 g/equiv.
- For Aluminum (Al):
- The n-factor for Al in Al(NO₃)₃ is 3 (since Al is in +3 oxidation state).
- Equivalent weight of Al = Atomic mass of Al / n-factor = 27.0 g/mol / 3 = 9.0 g/equiv.
3. Set Up the Ratio Using Faraday's Law:
- According to Faraday's law, the ratio of the weights of the substances deposited is equal to the ratio of their equivalent weights:
WCuWAl=ECuEAl
Where:
- WCu = weight of copper deposited
- WAl = weight of aluminum deposited
- ECu = equivalent weight of copper
- EAl = equivalent weight of aluminum
4. Substitute the Known Values:
WCu2.7g=31.75g/equiv.9.0g/equiv.
5. Cross-Multiply and Solve for WCu:
WCu=2.7g×31.759.0
WCu=2.7g×3.5278≈9.525g
6. Final Answer:
The weight of copper deposited on the cathode is approximately 9.525 g.
- Weight of aluminum deposited (W_Al) = 2.7 g
- Atomic mass of copper (Cu) = 63.5 g/mol
- Atomic mass of aluminum (Al) = 27.0 g/mol
- For Copper (Cu):
- The n-factor for Cu in Cu(NO₃)₂ is 2 (since Cu is in +2 oxidation state).
- Equivalent weight of Cu = Atomic mass of Cu / n-factor = 63.5 g/mol / 2 = 31.75 g/equiv.
- The n-factor for Al in Al(NO₃)₃ is 3 (since Al is in +3 oxidation state).
- Equivalent weight of Al = Atomic mass of Al / n-factor = 27.0 g/mol / 3 = 9.0 g/equiv.
- According to Faraday's law, the ratio of the weights of the substances deposited is equal to the ratio of their equivalent weights:
WCuWAl=ECuEAl
Where:
- WCu = weight of copper deposited
- WAl = weight of aluminum deposited
- ECu = equivalent weight of copper
- EAl = equivalent weight of aluminum
WCu2.7g=31.75g/equiv.9.0g/equiv.
WCu=2.7g×31.759.0
WCu=2.7g×3.5278≈9.525g
The weight of copper deposited on the cathode is approximately 9.525 g.
Similar Questions
When 0.1 Faraday of electricity is passed in aqueous solution of
AlCl3. The amount of Al deposited on cathode is
View Solution3F eletricity was passed through molten FeO. Weight of iron metal (Atomic wt=56) deposited at cathode (in g) is
View Solution2.5 amperes of current is passed through copper sulphate solution for 30 minutes. Calculate the number of copper atoms deposited at the cathode (Cu = 63.54).
View Solution(a) A steady current of 2 amperes was passed through two electrolytic cells X and Y connected in series containing electrolytes FeSO4 and ZnSO4 until 2.8 g of Fe deposited at the cathode of cell X. How long did the current flow ? Calculate the mass of Zn deposited at the cathode of cell Y
(Molar mass : Fe= 56 g mol−1 Zn-65.3g mol−1, 1F -96500 C mol−1)
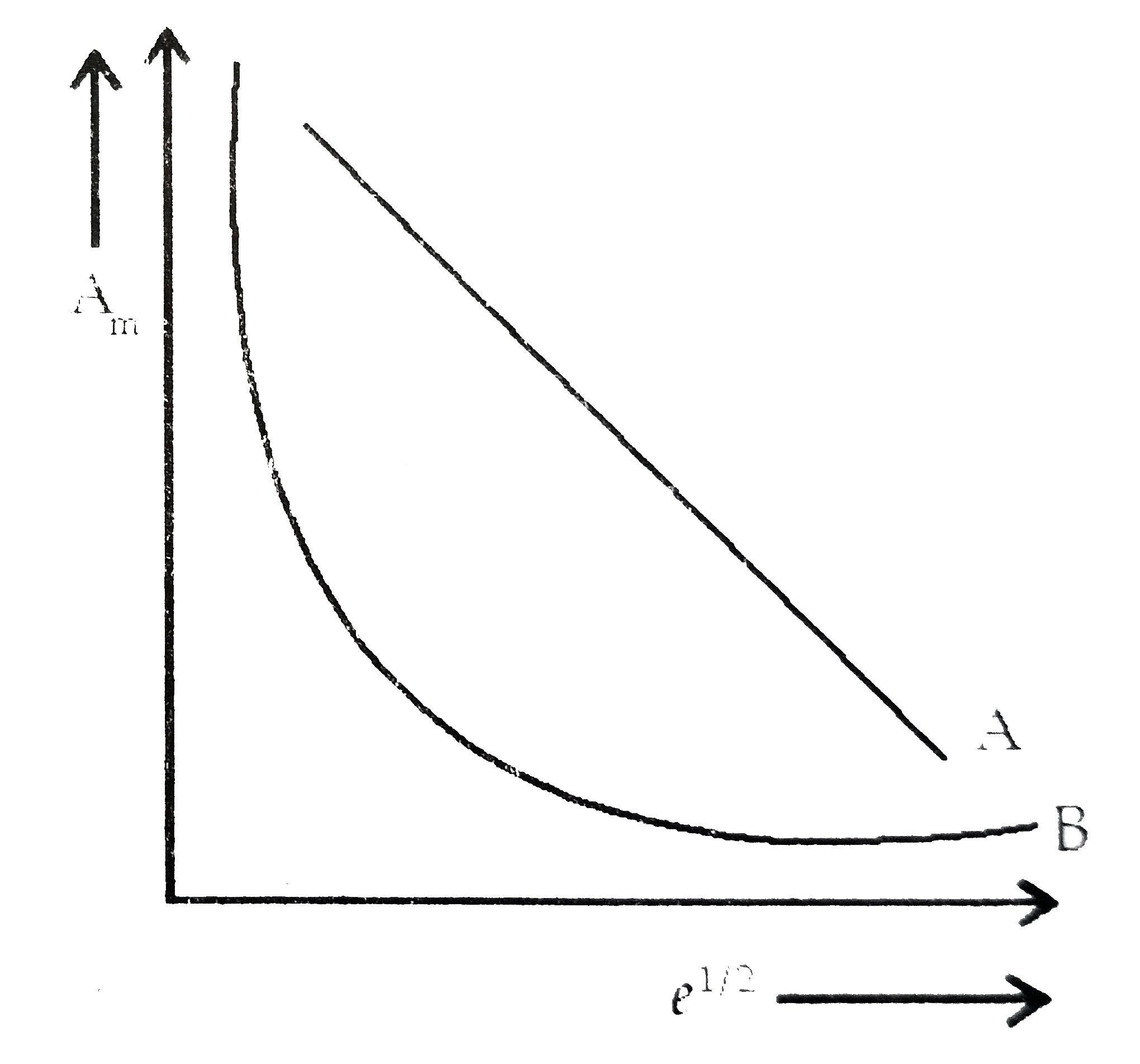
(b) In the plot of molar conductivity (∧m) vs Square root of concentration (c1/2), following curves are obtained for two electrolytes.
A and B:
Answer the following : (i) Predict the nature of electrolytes A and B. (ii) What happens on extrapolation of ∧m to concentration approaching zero for electrolytes A and B ?
View SolutionWhen 0.5 ampere of electricity is passed in aqueous solution of AgNO3 for 200 seconds, the amount of silver deposited on
cathode is (Z=0.00118gperC for Ag)
View SolutionOne Faraday of electricity is pa ssed through molten Al2O3, aqeusous solution of CuSO4 and molten NaCl taken in three different electrolytic cells connected in seris. The mole ratio of Al, Cu,Na deposted at the respective cathode is
View SolutionDuring electrolysis of an aqueous solution of CuSO4 using copper electrodes, if 2.5g of Cu is deposited at cathode, then at anode
View SolutionState True or False
The same quantity of electricity is passed through Al2(SO4)3 and AgNO3 solution with platinum electrodes. If n number of Al atoms are deposited on the cathode, 3n number of Ag atoms will be deposited on the cathode.
View SolutionA current of 0.1A was passed for 4hr through a solution of cuprocyanide and 0.3745 g of copper was deposited on the cathode. Calculate the current efficiency for the copper deposition. (Cu GAM 63.5 or Cu-63.5)
View SolutionWhat is the amount of Al deposited on the electrolysis of molten Al2O3 when a current of 9.65A is passed for 10.0s .
View Solution
