Two particles are projected from a point at the same instant with velocities whose horizontal and vertical components are u1,v1 and u2,v2 respectively. Prove that the interval between their passing through the other common point of their path is
2(v1u2−v2u1)g(u1+u2)
2g(v1u1−v2v2u1+u2)
2g(v21+v22u1+u2)
2g(u21+u22v1+v2)
2g(v1u2−v2u1u1+u2)
The correct Answer is:A
To solve the problem, we need to analyze the motion of two particles projected from the same point with given horizontal and vertical components of their velocities. We will derive the expression for the time interval between their passing through a common point in their paths.
1. Understanding the Motion:
- Let the horizontal components of the velocities of the two particles be u1 and u2.
- Let the vertical components of the velocities be v1 and v2.
- Both particles are projected from the origin (0, 0) at the same time.
2. Position of the Particles:
- The horizontal position x of the first particle at time t0 is given by:
x0=u1t0
- The horizontal position x of the second particle at time t0+Δt is:
x0=u2(t0+Δt)
3. Setting Up the Equation:
- Since both particles pass through the same point P(x0,y0), we can equate the two expressions for x0:
u1t0=u2(t0+Δt)
- Rearranging gives:
u1t0=u2t0+u2Δt
- This simplifies to:
(u1−u2)t0=u2Δt
- Thus, we can express Δt as:
Δt=(u1−u2)t0u2
4. Vertical Motion:
- The vertical position y of the first particle at time t0 is:
y0=v1t0−12gt20
- The vertical position y of the second particle at time t0+Δt is:
y0=v2(t0+Δt)−12g(t0+Δt)2
5. Equating Vertical Positions:
- Setting the two expressions for y0 equal gives:
v1t0−12gt20=v2(t0+Δt)−12g(t0+Δt)2
6. Expanding the Right Side:
- Expanding the right side:
v2t0+v2Δt−12g(t20+2t0Δt+Δt2)
- This leads to:
v1t0−12gt20=v2t0+v2Δt−12gt20−gt0Δt−12gΔt2
7. Simplifying the Equation:
- Canceling −12gt20 from both sides gives:
v1t0=v2t0+v2Δt−gt0Δt−12gΔt2
8. Rearranging:
- Rearranging for Δt:
(v1−v2)t0=(v2−gt0)Δt−12gΔt2
9. Final Expression:
- After some algebraic manipulation, we can derive the expression for Δt:
Δt=2(v1u2−v2u1)g(u1+u2)
10. Conclusion:
- Thus, we have proved that the interval between their passing through the common point of their path is:
Δt=2(v1u2−v2u1)g(u1+u2)
- Hence proved.
- Let the horizontal components of the velocities of the two particles be u1 and u2.
- Let the vertical components of the velocities be v1 and v2.
- Both particles are projected from the origin (0, 0) at the same time.
- The horizontal position x of the first particle at time t0 is given by:
x0=u1t0
- The horizontal position x of the second particle at time t0+Δt is:
x0=u2(t0+Δt)
- Since both particles pass through the same point P(x0,y0), we can equate the two expressions for x0:
u1t0=u2(t0+Δt)
- Rearranging gives:
u1t0=u2t0+u2Δt
- This simplifies to:
(u1−u2)t0=u2Δt
- Thus, we can express Δt as:
Δt=(u1−u2)t0u2
- The vertical position y of the first particle at time t0 is:
y0=v1t0−12gt20
- The vertical position y of the second particle at time t0+Δt is:
y0=v2(t0+Δt)−12g(t0+Δt)2
- Setting the two expressions for y0 equal gives:
v1t0−12gt20=v2(t0+Δt)−12g(t0+Δt)2
- Expanding the right side:
v2t0+v2Δt−12g(t20+2t0Δt+Δt2)
- This leads to:
v1t0−12gt20=v2t0+v2Δt−12gt20−gt0Δt−12gΔt2
- Canceling −12gt20 from both sides gives:
v1t0=v2t0+v2Δt−gt0Δt−12gΔt2
- Rearranging for Δt:
(v1−v2)t0=(v2−gt0)Δt−12gΔt2
- After some algebraic manipulation, we can derive the expression for Δt:
Δt=2(v1u2−v2u1)g(u1+u2)
- Thus, we have proved that the interval between their passing through the common point of their path is:
Δt=2(v1u2−v2u1)g(u1+u2)
- Hence proved.
Similar Questions
Two particles are projected simultaneously in the same vertical plane, with speed u1 and u2 at angle of projection θ1 and θ2 respectively with the horizontal. The path followed by one, as seen by other (as long as both are in flight), is
View SolutionThe numerical values and units of a physical quantity in two different system of units are n1,n2andu1,u2 respectively. Then
View SolutionIf v1 and v2 be the velocities at the end of focal chord of projectile path and u is the velocity at the vertex of the path, then
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
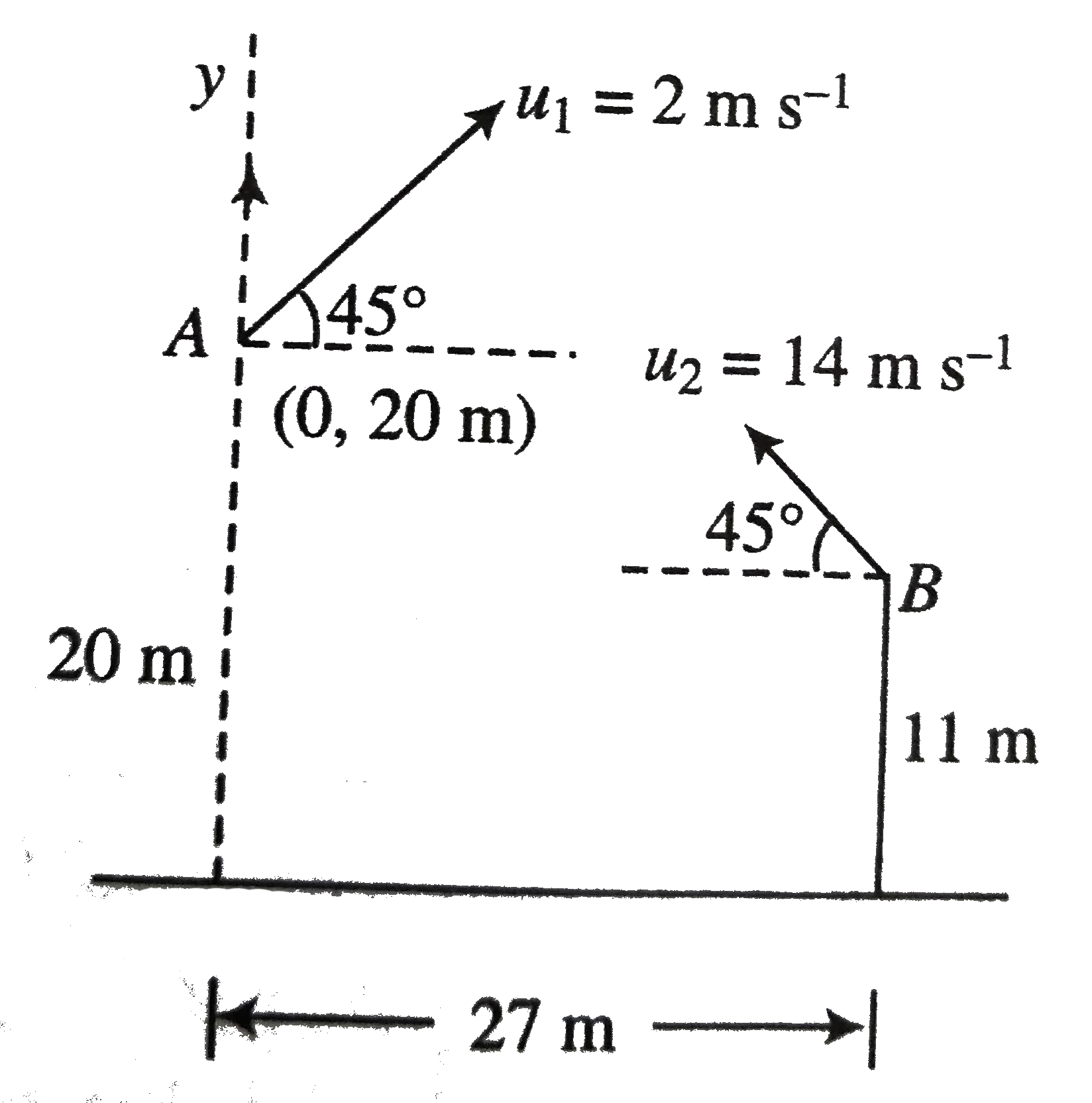
The relative velocity of B as seen from A in
View SolutionThe lateral magnification of the lens with an object located at two different position u1 and u2 are m1 and m2 , respectively. Then the focal length of the lens is
View SolutionThe molecular velocities of two gases at same temperature are u1 and u2, their masses are m1 and m2 respectively, which of the following expression is correct ?
View SolutionThe molecular velocities of two gases at same temperature are u1 and u2, their masses are m1 and m2 respectively, which of the following expression is correct ?
View SolutionFind the points of discontinuity of y=1u2+u−2, where u=1x−1
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
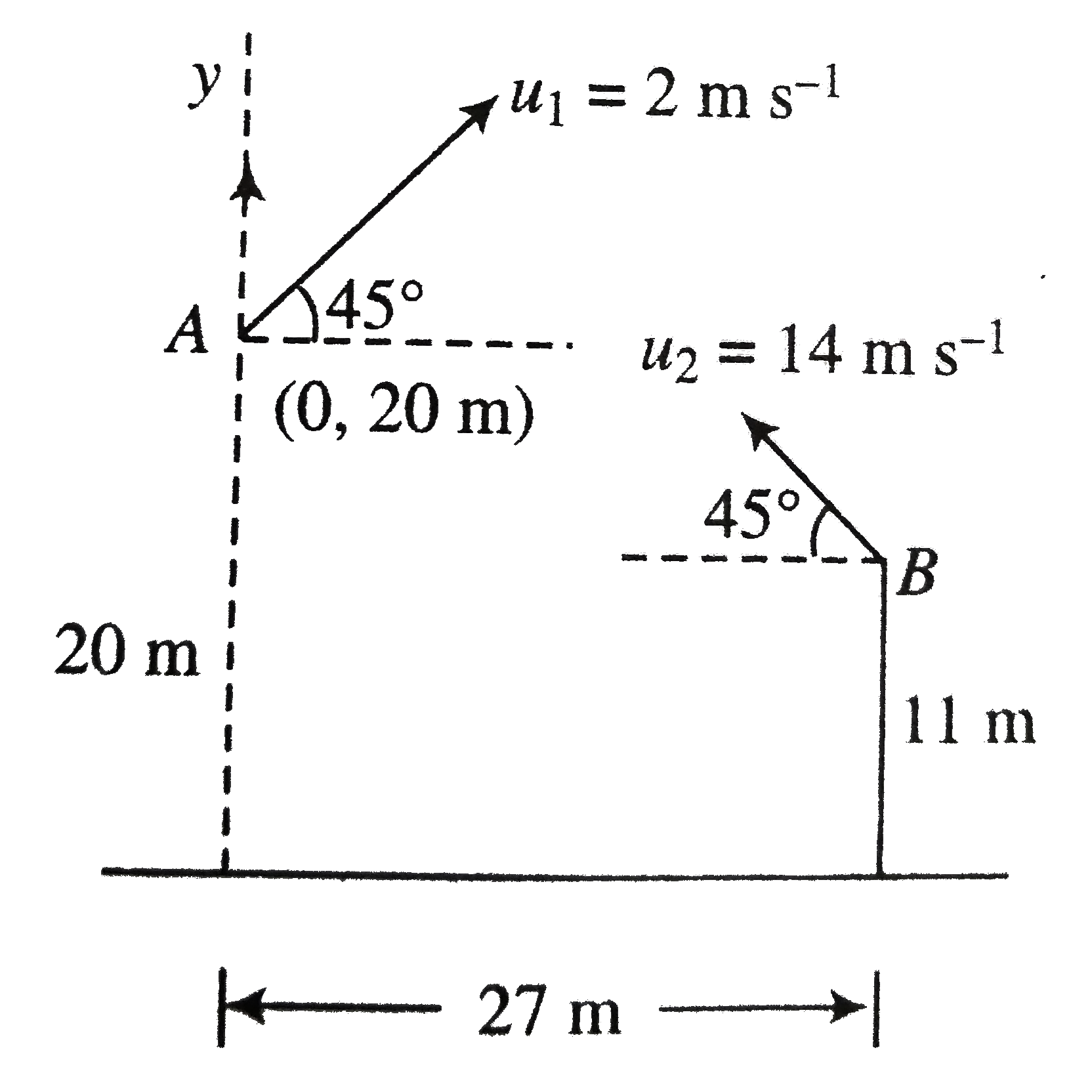
Minimum separation between A and B is
View SolutionTwo particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
View Solution
