A force →F=(5ˆi+3ˆj)N is applied over a particle which displaces it from its original position to the point →s=S(2ˆi−1ˆj)m. The work done on the particle is
−7J
+13J
+7J
+11J
The correct Answer is:C
To find the work done on the particle by the force, we can use the formula for work done, which is given by the dot product of the force vector and the displacement vector.
1. Identify the Force and Displacement Vectors:
- The force vector is given as:
→F=5^i+3^jN
- The displacement vector is given as:
→s=2^i−1^jm
2. Use the Work Done Formula:
- The work done W is calculated using the dot product of the force vector and the displacement vector:
W=→F⋅→s
3. Calculate the Dot Product:
- The dot product is calculated as follows:
W=(5^i+3^j)⋅(2^i−1^j)
- Expanding this, we get:
W=(5⋅2)+(3⋅−1)
- This simplifies to:
W=10−3
4. Final Calculation:
- Therefore, the work done is:
W=7J
Conclusion:
The work done on the particle is 7J.
- The force vector is given as:
→F=5^i+3^jN
- The displacement vector is given as:
→s=2^i−1^jm
- The work done W is calculated using the dot product of the force vector and the displacement vector:
W=→F⋅→s
- The dot product is calculated as follows:
W=(5^i+3^j)⋅(2^i−1^j)
- Expanding this, we get:
W=(5⋅2)+(3⋅−1)
- This simplifies to:
W=10−3
- Therefore, the work done is:
W=7J
The work done on the particle is 7J.
Similar Questions
A force →F=(5ˆi+3ˆj)N is applied over a particle which displaces it from its origin to the point →r=(2ˆi−1ˆj) meter. The work done on the particle is :
View SolutionA force →F=(5→i+3→j+2→k)N is applied over a particle which displaces it from its origin to the point →r=(2→i−→j)m. The work done on the particle in joules is.
View SolutionA constant force →F=(3ˆi+2ˆj+2ˆk) N acts on a particle displacing it from a position →r1=(−ˆi+ˆj−2ˆk)m to a new position →r2=(ˆi−ˆj+3ˆk)m. Find the work done by the force.
View SolutionA uniform force of (3ˆi+ˆj) N acts on a particle of mass 2kg. Hence, the particle is displaced from position (2ˆi+ˆk)m to position (4ˆi+3ˆj−ˆk)m. The work done by the force on the particle is
View SolutionWork done by a force F=(ˆi+2ˆj+3ˆk) acting on a particle in displacing it from the point r1=ˆi+ˆj+ˆk to the point r2=ˆi−ˆj+ˆ2k is
View SolutionA force (3ˆi+2ˆj) N displaces an object through a distance (2ˆi−3ˆj) m. The work done is :
View SolutionA force (3ˆi+2ˆj) N displaces an object through a distance (2ˆi−3ˆj) m. The work done is :
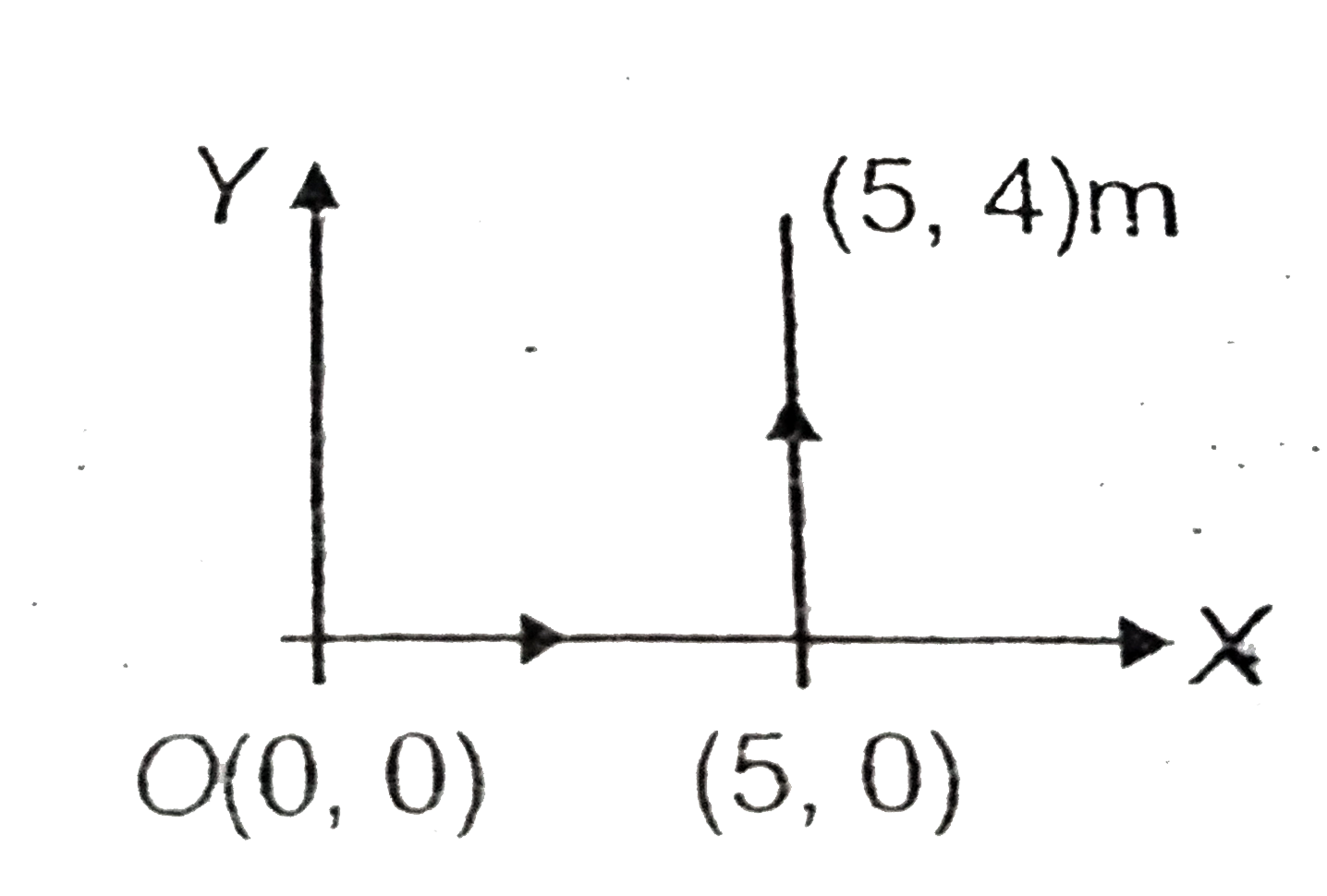
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA force →F=6xˆi+2yˆj displaces a body from →r1=3ˆi+8ˆj to →r2=5ˆi−4ˆj. Find the work done by the force.
View SolutionA particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
View Solution
