Consider a solid cube made up of insulating material having a uniform volume charge density. Assuming the electrostatic potential to be zero at infinity, the ratio of the potential at a corner of the cube to that at the centre will be
1:1
1:2
1:4
1:8
The correct Answer is:B
To solve the problem of finding the ratio of the electrostatic potential at a corner of a uniformly charged insulating cube to that at its center, we can follow these steps:
Step 1: Understanding the Geometry
Consider a solid cube of side length a with a uniform volume charge density ρ. The cube has 8 corners and a center point. We need to calculate the electrostatic potential at both the center and one of the corners.
Step 2: Calculate the Potential at the Center
The potential V due to a volume charge distribution is given by the formula:
V=14πϵ0∫ρdVr
where r is the distance from the charge element dV to the point where we are calculating the potential.
For the center of the cube, the distance from the center to any point inside the cube varies. However, due to symmetry, we can simplify our calculations. The distance from the center of the cube to the center of each face is a2.
The potential at the center V1 can be calculated as:
V1=ρ4πϵ0∫dV(a2)=ρ4πϵ0⋅8a3a2=16ρa24πϵ0
Step 3: Calculate the Potential at a Corner
Now, we calculate the potential at one of the corners of the cube. The distance from the center of the cube to a corner is given by:
r=√(a2)2+(a2)2+(a2)2=a√32
The potential at the corner V2 can be calculated similarly:
V2=ρ4πϵ0∫dV(a√32)=ρ4πϵ0⋅8a3a√32=16ρa24πϵ0√3
Step 4: Calculate the Ratio of Potentials
Now, we find the ratio of the potential at the corner to that at the center:
V2V1=16ρa24πϵ0√316ρa24πϵ0=1√3
Step 5: Final Result
Thus, the ratio of the potential at a corner of the cube to that at the center is:
V2V1=1√3
Consider a solid cube of side length a with a uniform volume charge density ρ. The cube has 8 corners and a center point. We need to calculate the electrostatic potential at both the center and one of the corners.
The potential V due to a volume charge distribution is given by the formula:
V=14πϵ0∫ρdVr
where r is the distance from the charge element dV to the point where we are calculating the potential.
V1=ρ4πϵ0∫dV(a2)=ρ4πϵ0⋅8a3a2=16ρa24πϵ0
Now, we calculate the potential at one of the corners of the cube. The distance from the center of the cube to a corner is given by:
r=√(a2)2+(a2)2+(a2)2=a√32
V2=ρ4πϵ0∫dV(a√32)=ρ4πϵ0⋅8a3a√32=16ρa24πϵ0√3
Now, we find the ratio of the potential at the corner to that at the center:
V2V1=16ρa24πϵ0√316ρa24πϵ0=1√3
Thus, the ratio of the potential at a corner of the cube to that at the center is:
V2V1=1√3
Similar Questions
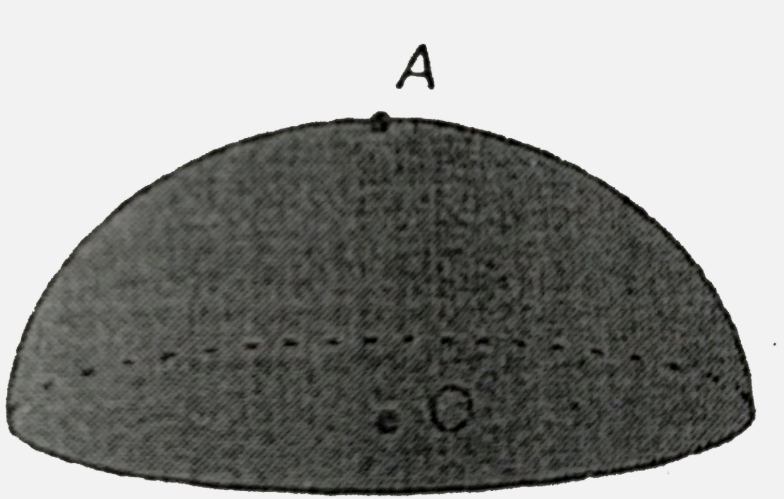
A hemispherical bowl of radius R carries a uniform surface charge density σ. Find the potential at the topmost point A, taking potential at infinity to be zero.
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from its surface at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionThere is a uniformly charged non conducting solid sphere made of amterial of dielectric constant one. If electric potenial at infinity be zero. Then the potential at its surface is V. if we take electric potential at its surface to be zero. Then the potential at the centre will be
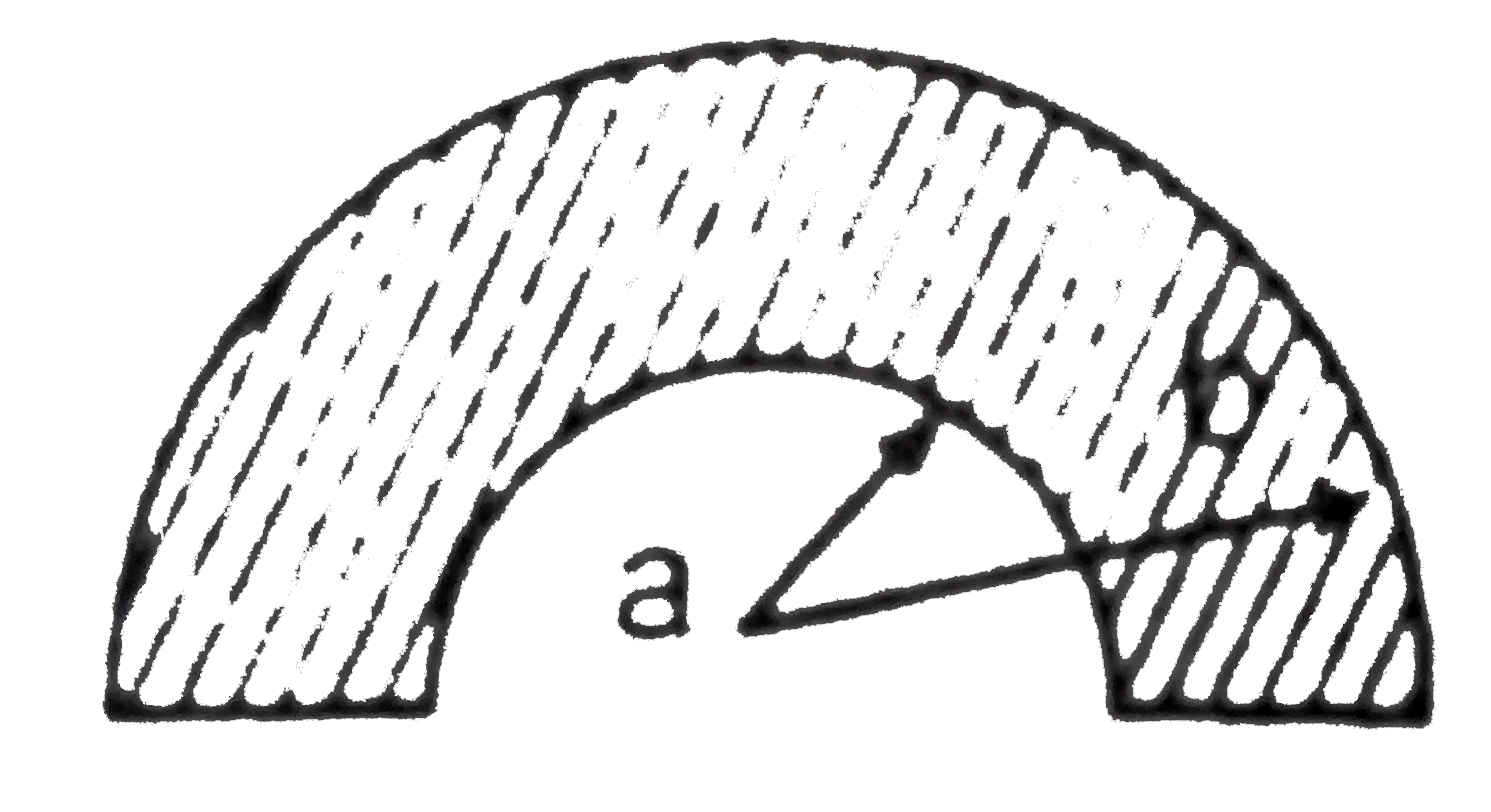
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View SolutionConsider a sphere of radius R having charge q uniformly distributed insider it. At what minimum distance from surface the electric potential is half of the electric potential at its centre?
View SolutionWhat is the ratio of the electrostatic potential at the corner and the centre point of a charged conducting cube? (The potential is considered 0 at infinity)
View Solution
