The Earth's atmosphere consists primarily of oxygen (21%) and nitrogen (78%). The rms speed of oxygen molecules (O2) in the atmosphere at a certain location is 535 m/s. The rms speed of the nitrogen molecules at this location will be [Given 1 amu =1.66×10−26 kg, molecular mass of O2=32, molecular mass of N2=28]
572 m/s
437 m/s
835 m/s
715 m/s
The correct Answer is:A
To find the root mean square (rms) speed of nitrogen molecules in the atmosphere, we can use the formula for rms speed:
vrms=√3RTM
where:
- R is the universal gas constant, R=8.314J/(mol K)
- T is the temperature in Kelvin
- M is the molar mass in kg/mol
Step 1: Calculate the Temperature (T)
We know the rms speed of oxygen (O2) is given as 535 m/s. We can use this information to find the temperature T.
Using the rms speed formula for oxygen:
vrms, O2=√3RTMO2
Substituting the known values:
535=√3×8.314×T32×10−3
Step 2: Square Both Sides
To eliminate the square root, we square both sides:
5352=3×8.314×T32×10−3
Calculating 5352:
287225=3×8.314×T0.032
Step 3: Rearranging the Equation
Now, rearranging the equation to solve for T:
T=287225×0.0323×8.314
Step 4: Calculate the Temperature (T)
Calculating T:
T=9171.224.942≈367.21K
Step 5: Calculate the rms Speed of Nitrogen (N2)
Now we will use the temperature T to find the rms speed of nitrogen (N2):
vrms, N2=√3RTMN2
Substituting the values:
vrms, N2=√3×8.314×367.2128×10−3
Step 6: Calculate the rms Speed of Nitrogen (N2)
Calculating vrms, N2:
vrms, N2=√3×8.314×367.210.028
Calculating the numerator:
3×8.314×367.21≈9171.2
Now substituting back:
vrms, N2=√9171.20.028≈√327,000≈571.93m/s
Step 7: Round the Answer
Rounding to a reasonable figure, we get:
vrms, N2≈572m/s
Final Answer
The rms speed of nitrogen molecules at this location is approximately 572 m/s.
---
- R is the universal gas constant, R=8.314J/(mol K)
- T is the temperature in Kelvin
- M is the molar mass in kg/mol
Similar Questions
Five molecules of a gas have speeds 1, 1, 3, 3, 2 km/s the value of the r.m.s spreed of the gas molecules is
View SolutionThe root-mean-square (rms) speed of oxygen molecules (O2) at a certain absolute temperature is v.If the temperature is double and the oxygen gas dissociated into atomic oxygen, the rms speed would be
View SolutionWhat mass of oxygen will contain 2 mol of O2 molecules? Molar mass of O2 is 32 gmol−1.
View SolutionFor a given gas at 1 atm pressure, rms speed of the molecules is 200m/s at 127∘C. At 2 atm pressure and at 227∘C, the speed of the molecules will be :
View SolutionAir consists mainly of nitrogen and oxygen molecules. Relative molecular masses of nitrogen and oxygen are 28 and 32 respectiely. Calculate :
(i) the ratio of the rms speed of nitrogen molecules to that of the oxygen molecules in air and
(ii) the ratio of the r.m.s. speed of oxygen molecules in air at 0∘C to that at 10∘C.
View SolutionAt what temperature , will the rms speed of oxygen molecules be sufficient for escaping from the earth ? Take m=2.76×10−26kg,k=1.38×10−23J/Kandve=11.2km/s.
View SolutionA flask contains hydrogen and helium in the ratio 2:1 by mass. The temperature of the mixture is 27∘C. Obtin the ratio of rms speeds of the molecules of the two gases. Atomic mass of hydrogen =2, molecular mass of helium =4
View SolutionThe rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
View SolutionThe rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
View SolutionThe following graphs shows two isothermal process for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at temperatures T1 and T2?
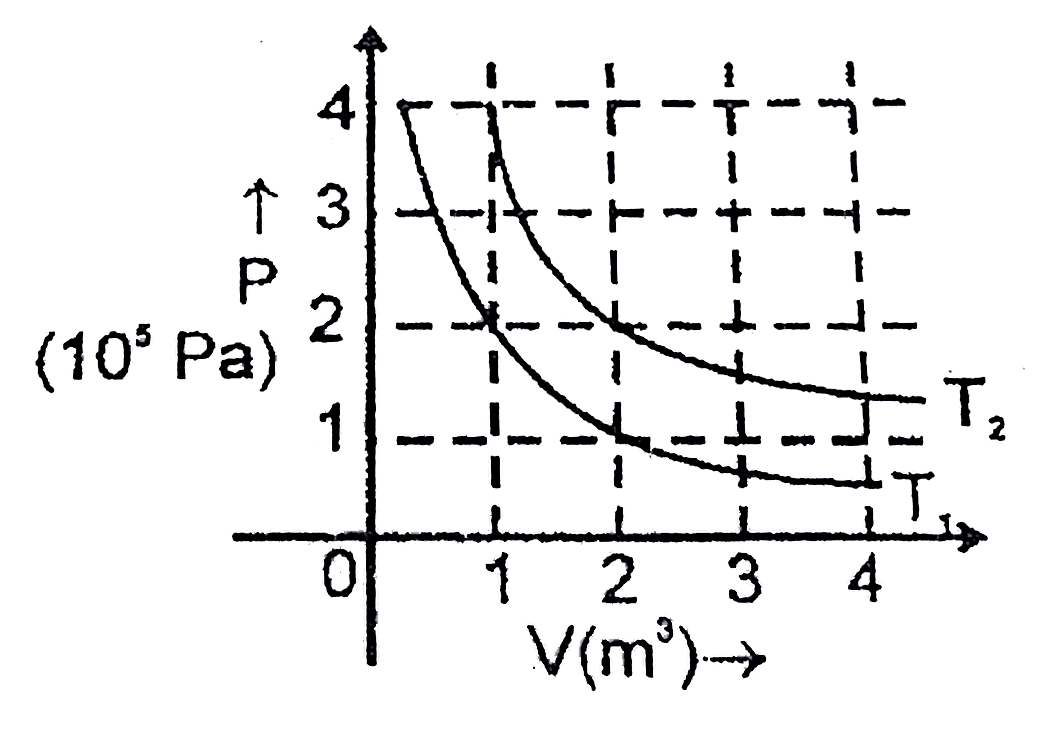
View Solution
