A glass hemisphere (μ=1.5) has a radius of curvature of 16 cm. A small object O is located on its axis halfway between the plane and spherical surface. The distance between two images , when viewed along the axis from the sides of the hemisphere is
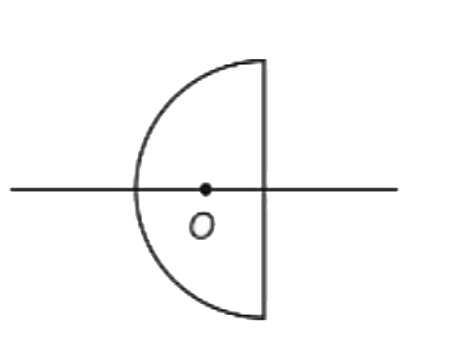
3215cm
4815cm
6415cm
8015cm
The correct Answer is:C
Step by step video & image solution for A glass hemisphere (mu=1.5) has a radius of curvature of 16 cm. A small object O is located on its axis halfway between the plane and spherical surface. The distance between two images , when viewed along the axis from the sides of the hemisphere is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A plastic hemisphere has a radius of curvature of 8 cm and an index of refraction of 1.6. ON the axis halfway between the plane surface and the spherical one (4 cm from each) is a small object O. The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately
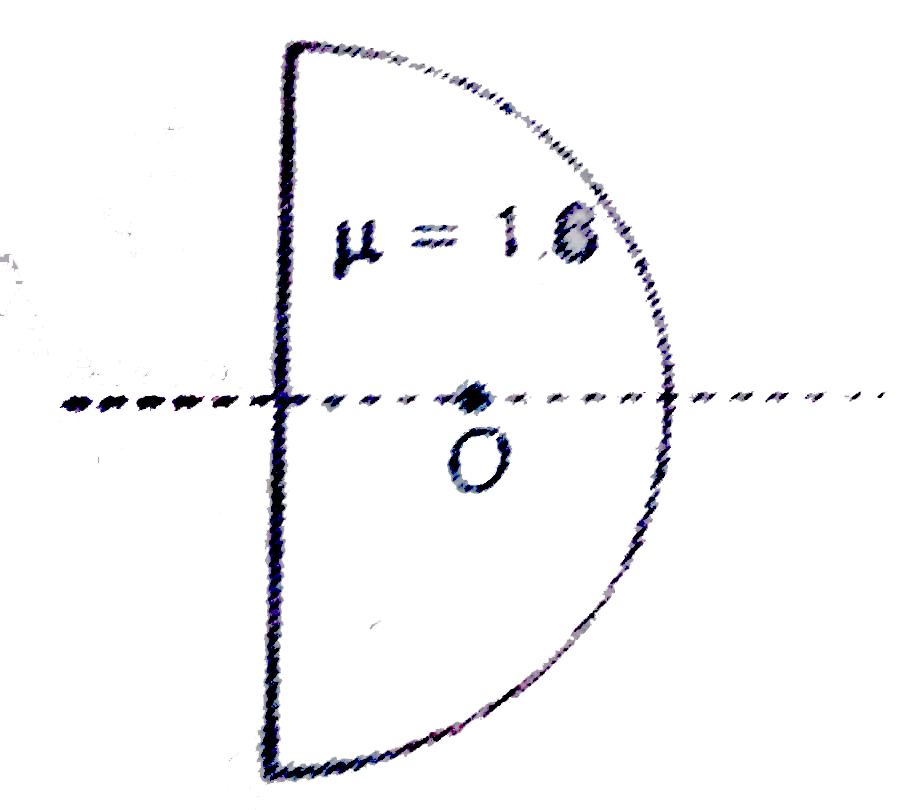View SolutionA plastic hemisphere has a radius of curvature of 8cm and an index of refraction of 1.6. On the axis halfway between the plane surface and the spherical one (4cm from each) is a small object O.
The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately.
View SolutionA solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
View SolutionFor a plane convex lens (μ=1.5) has radius of curvature 10 cm. It is slivered on its plane surface. Find focal length after silvering:
View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View SolutionA hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View SolutionA transpar ent rod 40 cm long is cut flat at one end and rounded to a hemispherical surface 12 cm radius at the other end. A small object is embedded within the rod along its axis and half way between its ends. When viewed from the flat end of the rod, the object appears 10 cm deep. What is its apparent depth when viewed from the curved end?
View SolutionThe radius of curvature of a convex mirror is 60cm. When an object is A, its image is formed at B. If the size of image is half that of the object, then the distance between A and B is
View SolutionIn figure , L is half part of an equiconvex glass lens (μ=1.5) whose surfaces have radius of curvature R =40cm and its right surface is silvered . Normal to its principal axis a plane mirror M is placed on right of the lens . Distance between lens L and mirror M is b. A small object O is placed on left of the lens such that there is no parallax between final images formed by the lens and mirror. If transverse length of final image formed by lens is twice that of image formed by the mirror , calculate distance'a' in cm between lens and object.
_S01_072_Q01.png)
View SolutionThe convex surface of a thin concave-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place ? (b) If the concave part is filled with water (mu = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.
View Solution