In a car race sound signals emitted by two cars are detected by the detector on the straight track at the end point of the race. Frequency observer is 330 Hz and 360 Hz and the original frequency is 300 Hz of both cars. Race ends with the separation of 100 m between the cars. Assume both cars move with constant velocity and velocity of sound is 330ms. Find the time taken by wining car.
The correct Answer is:4.00
To solve the problem, we need to find the time taken by the winning car in the race based on the frequencies detected and the original frequency of the sound emitted by both cars.
1. Identify Given Data:
- Original frequency of both cars, f0=300Hz
- Observed frequency from car A, f1=330Hz
- Observed frequency from car B, f2=360Hz
- Velocity of sound, v=330m/s
- Separation between the cars at the end of the race, d=100m
2. Use the Doppler Effect Formula:
The apparent frequency observed can be calculated using the Doppler effect formula for a source moving towards a stationary observer:
f′=f0vv−vs
Where:
- f′ is the observed frequency,
- f0 is the original frequency,
- v is the speed of sound,
- vs is the speed of the source (car).
3. Calculate the Speed of Car A:
For car A, using the observed frequency f1=330Hz:
330=300330330−v1
Rearranging gives:
330−v1=300⋅330330
Simplifying:
330−v1=300
Thus:
v1=330−300=30m/s
4. Calculate the Speed of Car B:
For car B, using the observed frequency f2=360Hz:
360=300330330−v2
Rearranging gives:
330−v2=300⋅330360
Simplifying:
330−v2=275
Thus:
v2=330−275=55m/s
5. Set Up the Equation for Distance:
The distance between the two cars is 100 m when car B reaches the endpoint. The time taken t can be calculated using the relative speeds of the two cars:
d=(v2−v1)⋅t
Substituting the values:
100=(55−30)⋅t
Simplifying gives:
100=25t
Thus:
t=10025=4s
Final Answer:
The time taken by the winning car is 4 seconds.
- Original frequency of both cars, f0=300Hz
- Observed frequency from car A, f1=330Hz
- Observed frequency from car B, f2=360Hz
- Velocity of sound, v=330m/s
- Separation between the cars at the end of the race, d=100m
The apparent frequency observed can be calculated using the Doppler effect formula for a source moving towards a stationary observer:
f′=f0vv−vs
Where:
- f′ is the observed frequency,
- f0 is the original frequency,
- v is the speed of sound,
- vs is the speed of the source (car).
For car A, using the observed frequency f1=330Hz:
330=300330330−v1
Rearranging gives:
330−v1=300⋅330330
Simplifying:
330−v1=300
Thus:
v1=330−300=30m/s
For car B, using the observed frequency f2=360Hz:
360=300330330−v2
Rearranging gives:
330−v2=300⋅330360
Simplifying:
330−v2=275
Thus:
v2=330−275=55m/s
The distance between the two cars is 100 m when car B reaches the endpoint. The time taken t can be calculated using the relative speeds of the two cars:
d=(v2−v1)⋅t
Substituting the values:
100=(55−30)⋅t
Simplifying gives:
100=25t
Thus:
t=10025=4s
The time taken by the winning car is 4 seconds.
Similar Questions
A siren emitting sound of frequency 800Hz is going away from a static listener with a speed of 30 m/s. Frequency of the sound to be heard by the listener is ( Take velocity of sound as 300 m/s )
View SolutionA policeman on duty detects a drop of 10% in the pitch of the horn of a moving car as it crosses him. If the velocity of sound is 330m/s, the speed of the car will be
View SolutionA policeman on duty detects a drop of 10% in the pitch of the hom of a motor car as it crosses him. If the velocity of sound is 330 m/s calculate the speed of car?
View SolutionThe frequency of a car horm is 400 Hz. If the horn is honked as the car moves with a speed uS=34ms through still air towards a stationary receiver, the wavelength of the sound passing the receiver is [velocity of sound is 340ms]
View Solution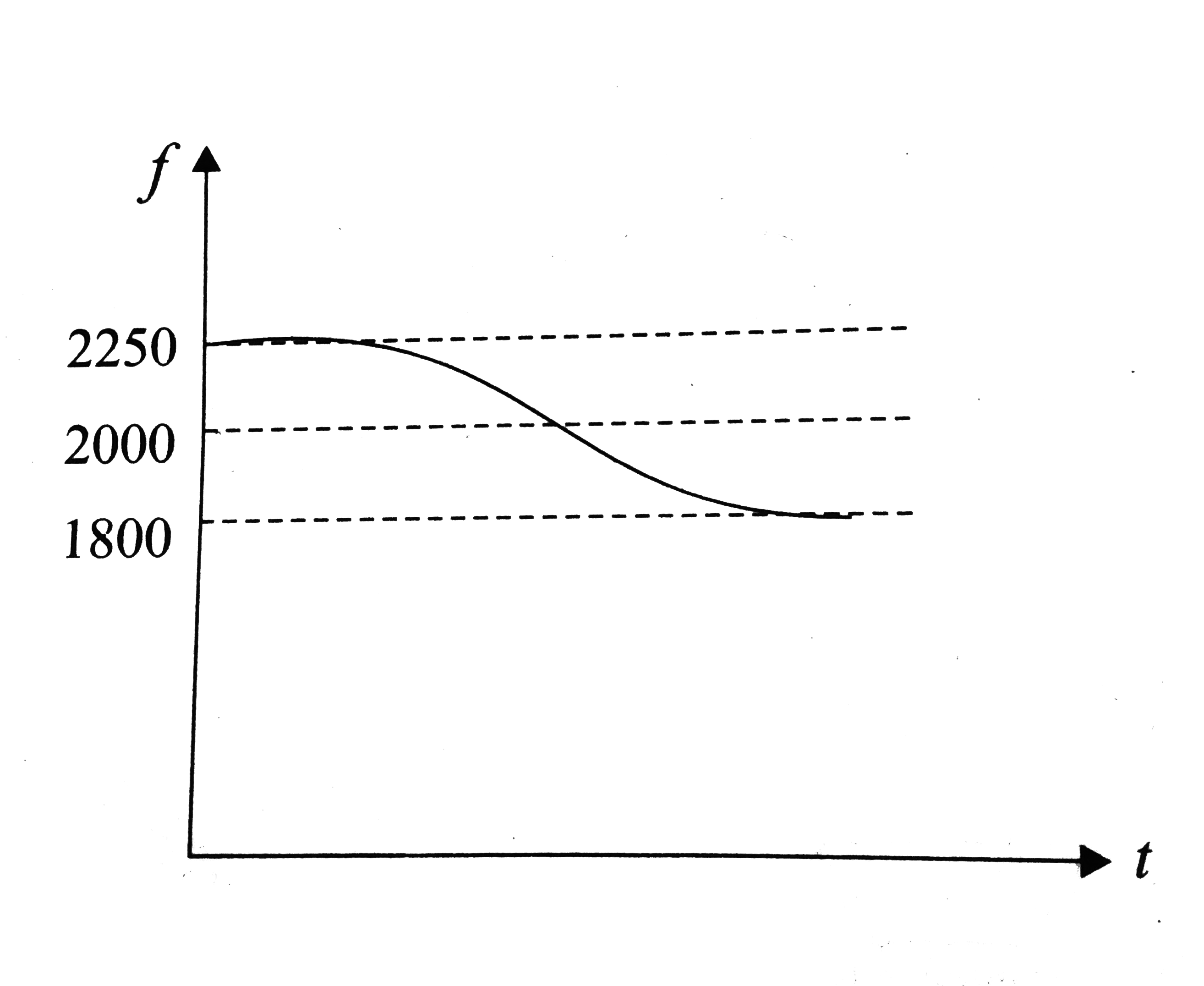
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionThe frequency of sound is 100 Hz and wavelength is 3m. Calculate the velocity of the wave.
View SolutionA police car horn emits a sound at a frequency 240 Hz. When the car is at rest. If the speed of the sound is 330 m/s the frequency heard by an observer who is approching the car at a speed of 11 m/s is
View SolutionThe ratio of the apparent frequencies of a car when approaching and receding a stationary observer is 11:9 What is the speed of the car, if the velocity of sound in air is 330 m/s?
View SolutionA car blowing a horn of frequency 350 Hz is moving normally towards a wall a speed of 5 m/s The beat frequency heard by a person standing between the car and wall is (speed of sound in air =350 m/s )
View SolutionA car moving at a speed of 72km/hr sounds its whistle which has a frequency of 550Hz, Find the frequencies heard by a stationary observer as the car approaches and then recedes from the observer, velocity of sound =340m/s.
View Solution