The magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of α.
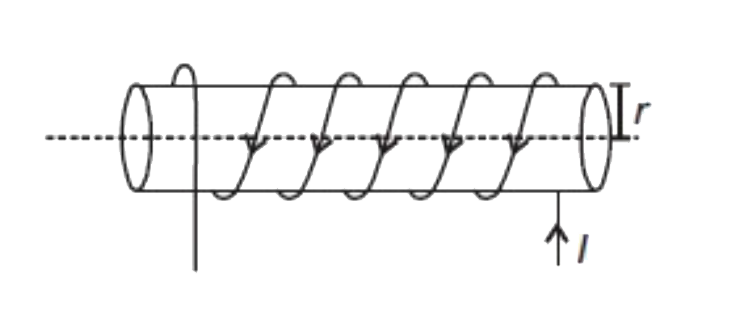
The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is
(a)√2πa2α
(b)12πa2α
(c)πa2α
(d)32πα
The correct Answer is:C
Step by step video & image solution for The magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of alpha. The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The magnetic energy stored in a long solenoid of area of cross-section A in a small region of length L is
View SolutionThe flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png)
View SolutionThe strength of magnetic field inside a long current-carrying straight solenoid is:
View SolutionThe magnetic field within cylindrical region whose cross - section is indicated starts increasing at a constant rate α tesla/sec . The graph showing the variation of induced field with distance r from the axis of cylinder is :

View SolutionWhen the current through a solenoid increases at a constant rate, the induced current in the solenoid
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionA solenoid 50 cm long has 4 layers of windings of 350 turns each. If the current carried is 6A. Find the magnetic field at the centre of the solenoid
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/m and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.01 As^(-1). The solenoid has 2000 turns/m and its radius 6.0 cm.
(a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds.
(b) find the electric field induced at a point on the circumference of the circle.
(c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View Solution
