The number of 7 digit integers abcdefg, where a<b<c<d>e>f>g such that a, b, c, d, e, f, g in {1,2,3,…..,9}. Are
700
20
720
800
The correct Answer is:C
To solve the problem of finding the number of 7-digit integers abcdefg such that a<b<c<d>e>f>g with a,b,c,d,e,f,g∈{1,2,3,…,9}, we can break it down into steps.
Step 1: Identify the constraints
We have the following constraints:
- a<b<c<d
- d>e>f>g
This means that a,b,c must be chosen from the numbers less than d, and e,f,g must be chosen from the numbers less than d but greater than d.
Step 2: Choose values for d
The value of d can be any number from 4 to 9 (since we need at least three numbers less than d for a,b,c and three numbers greater than d for e,f,g).
Step 3: Calculate combinations for each case of d
Case 1: d=4
- Possible values for a,b,c are from {1,2,3}.
- We can choose 3 numbers from these 3: (33)=1.
- No numbers are available for e,f,g since there are no numbers greater than 4.
- Total ways = 1×0=0.
Case 2: d=5
- Possible values for a,b,c are from {1,2,3,4}.
- Choose 3 from these 4: (43)=4.
- Possible values for e,f,g are from {6,7,8,9}.
- Choose 3 from these 4: (43)=4.
- Total ways = 4×4=16.
Case 3: d=6
- Possible values for a,b,c are from {1,2,3,4,5}.
- Choose 3 from these 5: (53)=10.
- Possible values for e,f,g are from {7,8,9}.
- Choose 3 from these 3: (33)=1.
- Total ways = 10×1=10.
Case 4: d=7
- Possible values for a,b,c are from {1,2,3,4,5,6}.
- Choose 3 from these 6: (63)=20.
- Possible values for e,f,g are from {8,9}.
- Choose 3 from these 2: (23)=0.
- Total ways = 20×0=0.
Case 5: d=8
- Possible values for a,b,c are from {1,2,3,4,5,6,7}.
- Choose 3 from these 7: (73)=35.
- Possible values for e,f,g are from {9}.
- Choose 3 from these 1: (13)=0.
- Total ways = 35×0=0.
Case 6: d=9
- Possible values for a,b,c are from {1,2,3,4,5,6,7,8}.
- Choose 3 from these 8: (83)=56.
- No numbers are available for e,f,g since there are no numbers greater than 9.
- Total ways = 56×0=0.
Step 4: Sum the total ways
Now we sum the total ways from each case:
- Total = 0+16+10+0+0+0=26.
Final Answer
The total number of 7-digit integers abcdefg satisfying the given conditions is 26.
We have the following constraints:
- a<b<c<d
- d>e>f>g
The value of d can be any number from 4 to 9 (since we need at least three numbers less than d for a,b,c and three numbers greater than d for e,f,g).
- Possible values for a,b,c are from {1,2,3}.
- We can choose 3 numbers from these 3: (33)=1.
- No numbers are available for e,f,g since there are no numbers greater than 4.
- Total ways = 1×0=0.
- Possible values for a,b,c are from {1,2,3,4}.
- Choose 3 from these 4: (43)=4.
- Possible values for e,f,g are from {6,7,8,9}.
- Choose 3 from these 4: (43)=4.
- Total ways = 4×4=16.
- Possible values for a,b,c are from {1,2,3,4,5}.
- Choose 3 from these 5: (53)=10.
- Possible values for e,f,g are from {7,8,9}.
- Choose 3 from these 3: (33)=1.
- Total ways = 10×1=10.
- Possible values for a,b,c are from {1,2,3,4,5,6}.
- Choose 3 from these 6: (63)=20.
- Possible values for e,f,g are from {8,9}.
- Choose 3 from these 2: (23)=0.
- Total ways = 20×0=0.
- Possible values for a,b,c are from {1,2,3,4,5,6,7}.
- Choose 3 from these 7: (73)=35.
- Possible values for e,f,g are from {9}.
- Choose 3 from these 1: (13)=0.
- Total ways = 35×0=0.
- Possible values for a,b,c are from {1,2,3,4,5,6,7,8}.
- Choose 3 from these 8: (83)=56.
- No numbers are available for e,f,g since there are no numbers greater than 9.
- Total ways = 56×0=0.
Now we sum the total ways from each case:
- Total = 0+16+10+0+0+0=26.
The total number of 7-digit integers abcdefg satisfying the given conditions is 26.
Similar Questions
If a<0andb<0, then (a+b)2>0.
View SolutionThe sum of all natural number 'n' such that 100<n<200 and H.C.F. (91,n)>1 is
View Solution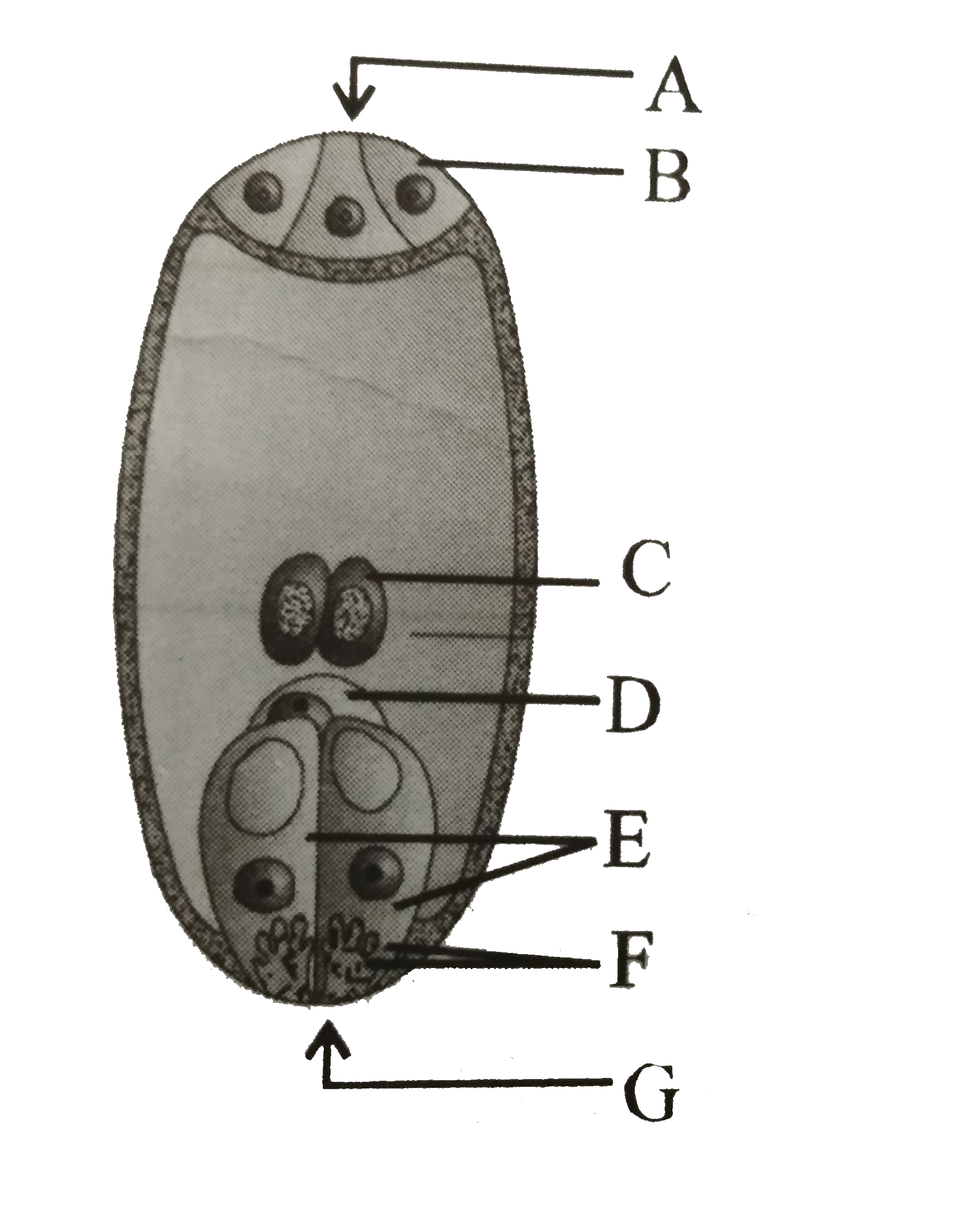
Identify A, B, C, D, E, F,G
View SolutionIf a , b, c, d are non-zero integers such that a<b<c<d and mean and median of a, b, c and d are both equal to zero, then which one of the following is correct?
View SolutionIf (x−a)(x−b)<0, then x<a,andx>b.
View SolutionState, whether the following statements are true of false.
If a<b,andc>0, then a−c>b−c where a, b, c and d are real number and c=!0.
View SolutionIf a and b are two negative integers such that a<b then 1a>1b.
View SolutionThere are five boys A, B, C, D and E. The order of their height is A<B<C<D<E. Number of ways in which they have to be arranged in four seats in increasing order of their height such that C and E are never adjacent.
View SolutionLet f (x) be a polynomial function of degree 3 where a<b<candf(a)=f(b)=f(c). If the graph of f (x) is as shown, which of the following statements are INCORRECT ? (Where c>|a|)

View SolutionIf the direction ratios of two lines are <a,b,c>and<b−c,c−a,a−b>, find the angle between them.
View Solution
