Two poles standing on horizontal ground are of heights 10 meters & 40 meters respectively. The line joining their tops makes an angle of with the ground. The the distance (in meters) between the foot of the poles is
20
30
The correct Answer is:D
To solve the problem, we need to find the distance between the feet of two poles of heights 10 meters and 40 meters, respectively, given that the line joining their tops makes an angle of 30 degrees with the ground.
1. Understanding the Setup:
- Let the height of the first pole (A) be 40 meters and the height of the second pole (B) be 10 meters.
- Let the foot of the first pole be point A and the foot of the second pole be point D.
- The tops of the poles are points C (top of pole A) and E (top of pole B).
2. Identifying the Triangle:
- The line joining the tops of the poles (CE) makes an angle of 30 degrees with the horizontal ground (AD).
- We can denote the distance between the feet of the poles (AD) as x.
3. Using Trigonometry:
- In triangle CDE, where D is the foot of the 10m pole and E is the foot of the 40m pole:
- The height difference (perpendicular) DE = 40m - 10m = 30m.
- The angle between the line CE and the horizontal is 30 degrees.
4. Applying Tangent Function:
- Using the tangent function for angle 30 degrees:
tan(30∘)=OppositeAdjacent=DEDB
- Here, DE = 30m (the height difference) and DB is the horizontal distance from D to the point directly below C (the foot of the 40m pole).
- We know that tan(30∘)=1√3, so:
30DB=1√3
- Rearranging gives:
DB=30√3
5. Finding the Distance AD:
- Now, we need to find the distance AD:
- In triangle ABC, where A is the top of the 40m pole and B is the top of the 10m pole:
- The height AC = 40m.
- Using the tangent function again:
tan(30∘)=ACAB
- Thus:
40AB=1√3
- Rearranging gives:
AB=40√3
6. Combining Distances:
- The total distance AD can be expressed as:
AD=DB+AB
- Substituting the values:
AD=30√3+10√3=40√3
7. Final Calculation:
- Therefore, the distance between the feet of the poles (AD) is:
AD=30√3 meters
Conclusion:
The distance between the foot of the poles is 30√3 meters.
- Let the height of the first pole (A) be 40 meters and the height of the second pole (B) be 10 meters.
- Let the foot of the first pole be point A and the foot of the second pole be point D.
- The tops of the poles are points C (top of pole A) and E (top of pole B).
- The line joining the tops of the poles (CE) makes an angle of 30 degrees with the horizontal ground (AD).
- We can denote the distance between the feet of the poles (AD) as x.
- In triangle CDE, where D is the foot of the 10m pole and E is the foot of the 40m pole:
- The height difference (perpendicular) DE = 40m - 10m = 30m.
- The angle between the line CE and the horizontal is 30 degrees.
- Using the tangent function for angle 30 degrees:
tan(30∘)=OppositeAdjacent=DEDB
- Here, DE = 30m (the height difference) and DB is the horizontal distance from D to the point directly below C (the foot of the 40m pole).
- We know that tan(30∘)=1√3, so:
30DB=1√3
- Rearranging gives:
DB=30√3
- Now, we need to find the distance AD:
- In triangle ABC, where A is the top of the 40m pole and B is the top of the 10m pole:
- The height AC = 40m.
- Using the tangent function again:
tan(30∘)=ACAB
- Thus:
40AB=1√3
- Rearranging gives:
AB=40√3
- The total distance AD can be expressed as:
AD=DB+AB
- Substituting the values:
AD=30√3+10√3=40√3
- Therefore, the distance between the feet of the poles (AD) is:
AD=30√3 meters
The distance between the foot of the poles is 30√3 meters.
Similar Questions
Two poles standing on a horizontal ground are of height x meters and 40 meters respectively. The line joining their tops makes an angle of 30∘ with the ground and the distance between the foot of the poles is 30√3 meters, then the value of x can be
View SolutionTwo poles standing on a horizontal ground are of heights 5 m and 10 m, respectively. The line joining their tops makes an angle of 15∘ with the ground. Then, the distance (in m) between the poles, is
View Solution
Knowledge Check
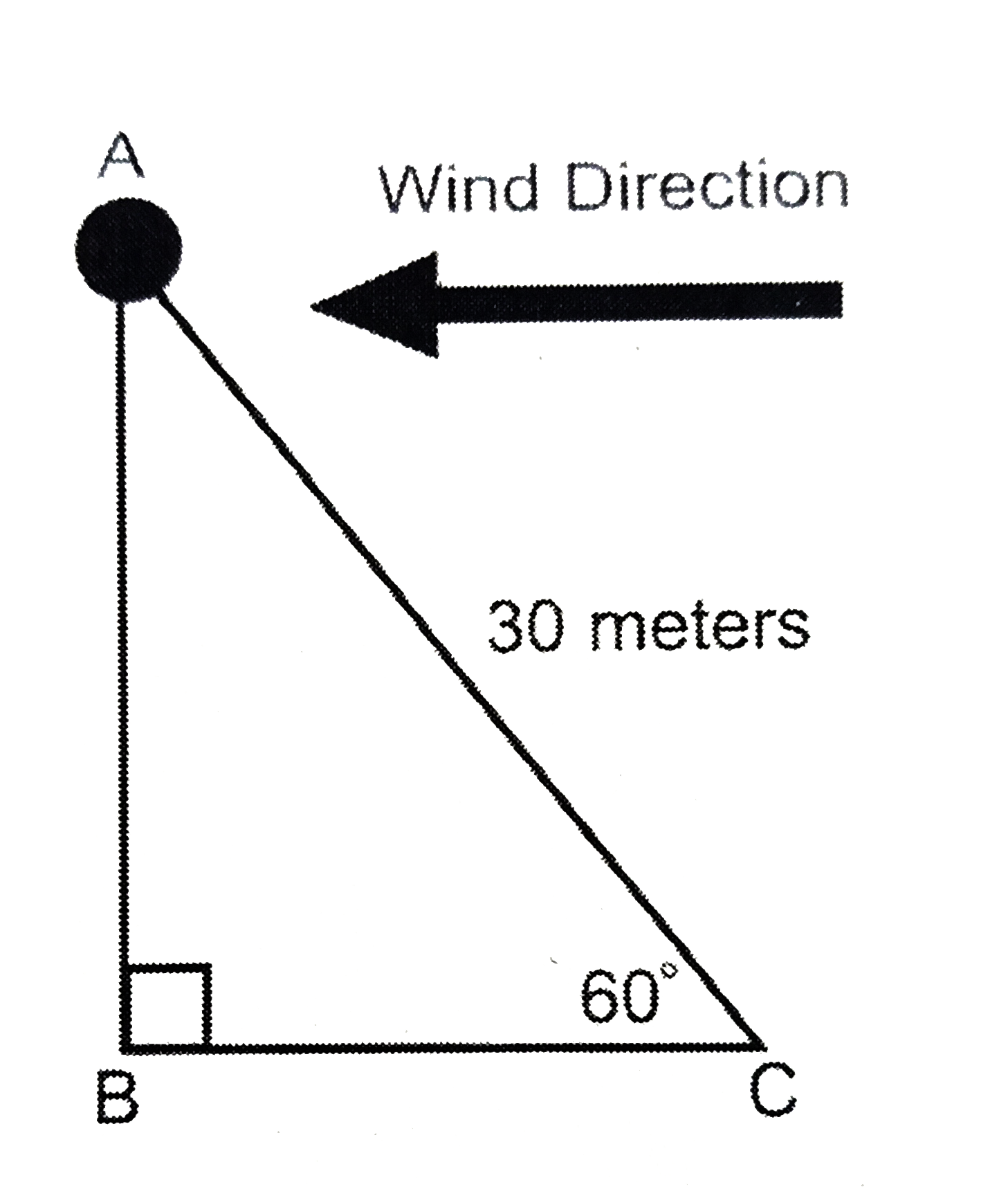
A hot air balloon was tied to a point on the ground using a rope 60m long. If the rope makes an angle of 60∘ with the ground, how high, in meters, is the balloon above the ground level?A30√3B30C60√3D30√3
The tops of two poles of height 40 m and 25 m are connected by a wire. If the wire makes an angle 30∘ with the horizontal, then the length of the wire is
View SolutionA tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30o with the ground. The distance between the foot of the tree to the point where the top touches the ground is 10m. Find the height of the tree.
View SolutionA tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30o with the ground. The distance between the foot of the tree to the point where the top touches the ground is 8m. Find the height of the tree.
View SolutionTwo vertical poles of height 10 m and 40 m stand apart on a horizontal plane. The height (in meters) of the point of intersection of the line joining the top of each pole to the foot of the other, from this horizontal plane is
View SolutionTwo poles of height 6 meters and 11 meteras stand vertically on a plane ground. If the distance between their feet is 12 meters. Find the distance between their tops.
View SolutionThe angle of elevation of the bottom of a window 10 m above the ground level from a point on the ground is 30∘ A pole projecting outwards from the bottom of the window makes an angle of 30∘ with the wall. If the angle of elevation of the top of the pole observed from the same point on the ground is 60∘, find the length of the pole to the nearest whole number.
View SolutionAn object is projected horizontally from a top of the tower of height h. The line joining the point of projection and point of striking on the ground makes an angle 45∘ with ground, then with what velocity the object strikes the ground
View Solution
