Two circles of radii r1andr2, are both touching the coordinate axes and intersecting each other orthogonally. The value of r1r2 (where r1>r2) equals -
2
2+√3
3+√2
3
The correct Answer is:B
To solve the problem, we need to find the ratio r1r2 for two circles that touch the coordinate axes and intersect orthogonally. Here’s a step-by-step solution:
Step 1: Understand the Position of the Circles
Both circles touch the coordinate axes. Therefore, the centers of the circles will be at the coordinates:
- For the smaller circle with radius r2: Center at (r2,r2)
- For the larger circle with radius r1: Center at (r1,r1)
Step 2: Write the Equations of the Circles
The equation of a circle in standard form is given by:
(x−h)2+(y−k)2=r2
where (h,k) is the center and r is the radius.
For the smaller circle:
(x−r2)2+(y−r2)2=r22
Expanding this gives:
x2−2r2x+r22+y2−2r2y+r22=r22
Simplifying, we have:
x2+y2−2r2x−2r2y+r22=0(Equation 1)
For the larger circle:
(x−r1)2+(y−r1)2=r21
Expanding this gives:
x2−2r1x+r21+y2−2r1y+r21=r21
Simplifying, we have:
x2+y2−2r1x−2r1y+r21=0(Equation 2)
Step 3: Use the Condition of Orthogonality
The circles intersect orthogonally if:
2f1f2+2g1g2=c1+c2
From the equations:
- For the smaller circle (Equation 1):
- g1=−r2, f1=−r2, c1=r22
- For the larger circle (Equation 2):
- g2=−r1, f2=−r1, c2=r21
Substituting these into the orthogonality condition:
2(−r2)(−r1)+2(−r2)(−r1)=r22+r21
This simplifies to:
4r1r2=r21+r22
Step 4: Rearranging the Equation
Rearranging gives:
r21−4r1r2+r22=0
Step 5: Let x=r1r2
Substituting r1=xr2 into the equation:
(xr2)2−4(xr2)(r2)+r22=0
This simplifies to:
x2r22−4xr22+r22=0
Dividing through by r22 (since r2≠0):
x2−4x+1=0
Step 6: Solve the Quadratic Equation
Using the quadratic formula:
x=−b±√b2−4ac2a=4±√16−42=4±√122=4±2√32=2±√3
Step 7: Determine the Correct Ratio
Since r1>r2, we take the positive value:
r1r2=2+√3
Final Answer
Thus, the value of r1r2 is:
r1r2=2+√3
---
Both circles touch the coordinate axes. Therefore, the centers of the circles will be at the coordinates:
- For the smaller circle with radius r2: Center at (r2,r2)
- For the larger circle with radius r1: Center at (r1,r1)
The equation of a circle in standard form is given by:
(x−h)2+(y−k)2=r2
where (h,k) is the center and r is the radius.
(x−r2)2+(y−r2)2=r22
Expanding this gives:
x2−2r2x+r22+y2−2r2y+r22=r22
Simplifying, we have:
x2+y2−2r2x−2r2y+r22=0(Equation 1)
(x−r1)2+(y−r1)2=r21
Expanding this gives:
x2−2r1x+r21+y2−2r1y+r21=r21
Simplifying, we have:
x2+y2−2r1x−2r1y+r21=0(Equation 2)
The circles intersect orthogonally if:
2f1f2+2g1g2=c1+c2
From the equations:
- For the smaller circle (Equation 1):
- g1=−r2, f1=−r2, c1=r22
- For the larger circle (Equation 2):
- g2=−r1, f2=−r1, c2=r21
2(−r2)(−r1)+2(−r2)(−r1)=r22+r21
This simplifies to:
4r1r2=r21+r22
Rearranging gives:
r21−4r1r2+r22=0
Substituting r1=xr2 into the equation:
(xr2)2−4(xr2)(r2)+r22=0
This simplifies to:
x2r22−4xr22+r22=0
Dividing through by r22 (since r2≠0):
x2−4x+1=0
Using the quadratic formula:
x=−b±√b2−4ac2a=4±√16−42=4±√122=4±2√32=2±√3
Since r1>r2, we take the positive value:
r1r2=2+√3
Thus, the value of r1r2 is:
r1r2=2+√3
Similar Questions
The circles having radii r1andr2 intersect orthogonally. Find the length of their common chord.
View SolutionThe value of b−cr1+c−ar2+a−br3 is equal to
View SolutionTwo circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
View SolutionTwo circles centres AandB radii r1andr2 respectively. (i) touch each other internally iff |r1−r2|=AB. (ii) Intersect each other at two points iff |r1−r2|<AB<r1+r2. (iii) touch each other externally iff r1+r2=AB. (iv) are separated if AB>r1+r2. Number of common tangents to the two circles in case (i), (ii), (iii) and (iv) are 1, 2, 3 and 4 respectively. If circles (x−1)2+(y−3)2=r2andx2+y2−8x+2y+8=0 intersect each other at two different points, then : (A) 1<r<5 (B) 5<r<8 (C) 2<r<8 (D) none of these
View SolutionTwo circles centres AandB radii r1andr2 respectively. (i) touch each other internally iff |r1−r2|=AB. (ii) Intersect each other at two points iff |r1−r2|<AB<r1r2. (iii) touch each other externally iff r1+r2=AB. (iv) are separated if AB>r1+r2. Number of common tangents to the two circles in case (i), (ii), (iii) and (iv) are 1, 2, 3 and 4 respectively. Number of common tangents to the circles x2+y2−6x=0andx2+y2+2x=0 is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionTwo circles centres AandB radii r1andr2 respectively. (i) touch each other internally iff |r1−r2|=AB. (ii) Intersect each other at two points iff |r1−r2|<AB<r1r2. (iii) touch each other externally iff r1+r2=AB. (iv) are separated if AB>r1+r2. Number of common tangents to the two circles in case (i), (ii), (iii) and (iv) are 1, 2, 3 and 4 respectively. circles x2+y2+2ax+c2=0andx2+y2+2by+c2=0 touche each other if (A) 1a2+1b2=2c2 (B) 1a2+1b2=2c2 (C) 1a2−1b2=2c2 (D) 1a2−1b2=4c2
View SolutionTwo circle of radii R and r,R>r touch each other externally then the radius of circle which touches both of them externally and also their direct common tangent, is R (b) RrR+r Rr(√R+√r)2 (d) Rr(√R−√r)2
View Solutionr+r3+r1−r2=
View SolutionLet two circles having radii r1andr2 are orthogonal to each other. If the length of their common chord is k times the square root of harmonic mean between the squares of their radii, then k4 is equal to
View SolutionTwo soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
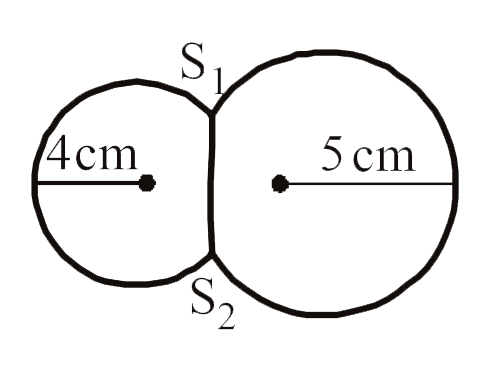
View Solution