A car is moving along the circle x2+y2=a2 in the anti-clockwise direction with a constant speed. The x-y plane is a rough horizontal stationary surface. When the car is at the point (acosθ,asinθ), the unit vector in the direction of the friction force acting on the car is
cosθˆi+sinθˆi
cosθˆi+sinθˆi
−cosθˆi−sinθˆj
−cosθˆi+sinθˆj
The correct Answer is:C
To solve the problem, we need to determine the unit vector in the direction of the friction force acting on the car as it moves along the circular path defined by the equation x2+y2=a2. The car is at the point (acosθ,asinθ).
1. Understanding the Motion: The car is moving in a circular path with a constant speed in the anti-clockwise direction. The position of the car at any instant is given by the coordinates (acosθ,asinθ).
2. Centripetal Force: Since the car is moving in a circle, it requires a centripetal force to keep it in circular motion. In this case, the friction force acts as the centripetal force.
3. Direction of the Friction Force: The friction force must act towards the center of the circle to provide the necessary centripetal force. The center of the circle is at the origin (0,0).
4. Finding the Vector from the Point to the Center: The position vector of the car at the point (acosθ,asinθ) can be represented as:
r=acosθ^i+asinθ^j
The vector pointing from the car to the center (origin) is:
Ffriction=0−(acosθ^i+asinθ^j)=−acosθ^i−asinθ^j
5. Finding the Unit Vector: To find the unit vector in the direction of the friction force, we need to divide the friction force vector by its magnitude. The magnitude of the friction force vector is:
|Ffriction|=√(−acosθ)2+(−asinθ)2=√a2(cos2θ+sin2θ)=a
Therefore, the unit vector in the direction of the friction force is:
^Ffriction=Ffriction|Ffriction|=−acosθ^i−asinθ^ja=−cosθ^i−sinθ^j
6. Final Result: Thus, the unit vector in the direction of the friction force acting on the car is:
^Ffriction=−cosθ^i−sinθ^j
r=acosθ^i+asinθ^j
The vector pointing from the car to the center (origin) is:
Ffriction=0−(acosθ^i+asinθ^j)=−acosθ^i−asinθ^j
|Ffriction|=√(−acosθ)2+(−asinθ)2=√a2(cos2θ+sin2θ)=a
Therefore, the unit vector in the direction of the friction force is:
^Ffriction=Ffriction|Ffriction|=−acosθ^i−asinθ^ja=−cosθ^i−sinθ^j
^Ffriction=−cosθ^i−sinθ^j
Similar Questions
The centre of the circle x=2+3cosθ,y=3sinθ−1, is
View SolutionTwo thin roads are moving perpendicularly as shown in the figure. If the friction acting between them is FR then the unit vector in the direction of friction force acting on the rod lying along x-axis is
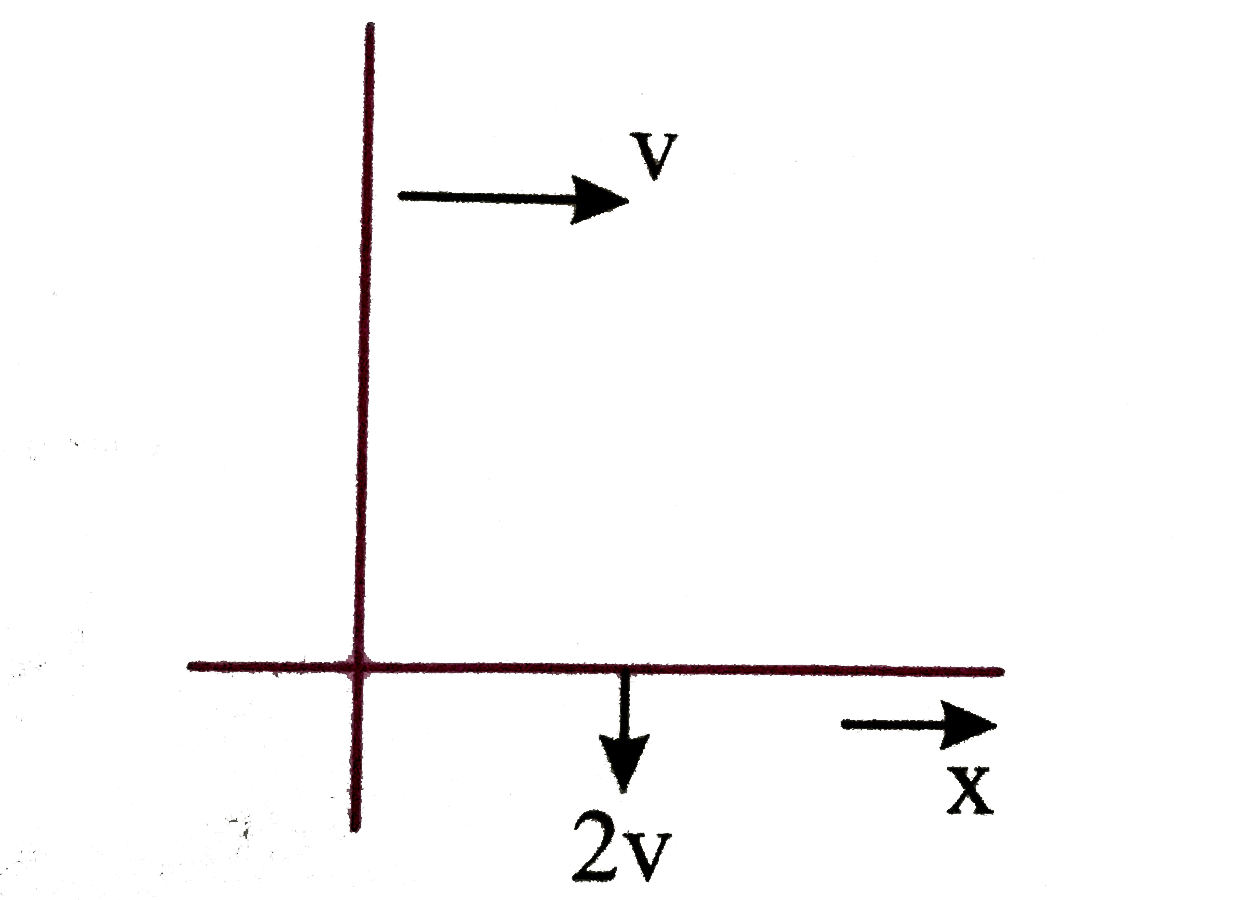 View Solution
View SolutionIf x=3+2cosθ,y=5+2sinθ then the locus of the point (x,y) is a circle with centre and radius
View SolutionShow that the point (x,y) , where x=5cosθ,y=−3+5sinθ, lies on a circle for all values of theta
View SolutionIf xcosθ+ysinθ=2 is perpendicular to the line x-y =3 then what is one of the value of θ?
View SolutionIf x=3cosθ−2cos3θ,y=3sinθ−2sin3θ, then dydx is
View Solutiontangents are drawn to x2+y2=a2 at the points A(acosθ,asinθ) and B(acos(θ+π3),asin(θ+π3)) Locus of intersection of these tangents is
View Solutionif x=cosθ−cos2θ,y=sinθ−sin2θ, then dy/dx is
View SolutionShow that the point (x,y), where x=a+rcosθ,y=b+rsinθ, lies on a circle for all values of θ.
View SolutionIf xsin3θ+ycos3θ=sinθcosθandxsinθ=ycosθ, Find the value of x2+y2.
View Solution

