If the radii of nuclei of are respectively, then
The correct Answer is:B
To solve the problem of finding the ratio of the radii of the nuclei of Aluminum and Zinc, we can follow these steps:
Step 1: Understand the relationship between volume and mass number
The volume of a nucleus is directly proportional to its mass number (A). This means:
V∝A
Step 2: Express the volume of a spherical nucleus
The volume (V) of a spherical nucleus can be expressed as:
V=43πR3
where R is the radius of the nucleus.
Step 3: Relate volume to mass number
From the above, we can say:
43πR3∝A
Since 43π is a constant, we can simplify this to:
R3∝A
Step 4: Establish the relationship between radius and mass number
From the proportionality, we can express the radius in terms of mass number:
R∝A1/3
Step 5: Write the expressions for the radii of Aluminum and Zinc
Let R1 be the radius of Aluminum-27 and R2 be the radius of Zinc-64. We can write:
R1∝A1/31
R2∝A1/32
where A1=27 (mass number of Aluminum) and A2=64 (mass number of Zinc).
Step 6: Formulate the ratio of the radii
Now, we can write the ratio of the radii:
R1R2=A1/31A1/32
Step 7: Substitute the mass numbers
Substituting the values of A1 and A2:
R1R2=271/3641/3
Step 8: Simplify the expression
We can simplify this further:
R1R2=(2764)1/3
Step 9: Calculate the cube root
Calculating the cube root:
2764=(34)3
Thus:
(2764)1/3=34
Final Answer
Therefore, the ratio of the radii of the nuclei of Aluminum and Zinc is:
R1R2=34
The volume of a nucleus is directly proportional to its mass number (A). This means:
V∝A
The volume (V) of a spherical nucleus can be expressed as:
V=43πR3
where R is the radius of the nucleus.
From the above, we can say:
43πR3∝A
Since 43π is a constant, we can simplify this to:
R3∝A
From the proportionality, we can express the radius in terms of mass number:
R∝A1/3
Let R1 be the radius of Aluminum-27 and R2 be the radius of Zinc-64. We can write:
R1∝A1/31
R2∝A1/32
where A1=27 (mass number of Aluminum) and A2=64 (mass number of Zinc).
Now, we can write the ratio of the radii:
R1R2=A1/31A1/32
Substituting the values of A1 and A2:
R1R2=271/3641/3
We can simplify this further:
R1R2=(2764)1/3
Calculating the cube root:
2764=(34)3
Thus:
(2764)1/3=34
Therefore, the ratio of the radii of the nuclei of Aluminum and Zinc is:
R1R2=34
Similar Questions
Two spherical nuclei have mass number 216 and 64 with their radii R1andR2 respectively. The ratio, R1R2 is equal to
View SolutionThe ratio of the radii of the nuclei .2713Al and .52Te125 is approximately-
View SolutionTwo spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionIf radii of the smallest and the largest circle passing through (√3,√2) and touching the circle x2+y2−2√2y−2=0 are r1 and r2 respectively, then find the mean of r1 and r2.
View SolutionFig shows three resistor configuration R1,R2andR3 connected to 3V battery. If the power dissipated by the configuration R1,R2andR3 is P1,P2andP3 respectively, then
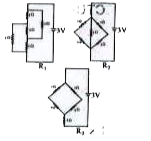
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
View SolutionTwo soap bubbles are stuck together with an intermediate film separating them. Compute the radius of curvature of this film given that the radii of the bubbles in this arrangement are r1 and r2 respectively. If r1>r2 state clearly which way the intermediate film will bulge.
For the case when r1=r2=2cm calculate he radius of the bubble formed by bursting the intermediate film. The volume of a spherical dome of radius R and height h is πb2(3R−b)/3.
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
View SolutionIn △ABC, If r1,r2,r3 are exradii opposites to angles A,B and C respectively. Then (1r1+1r2)(1r2+1r3)(1r3+1r1) is equal to
View Solution
