A ball is dropped on a smooth inclined plane and is observed to move horizontally after the impact. The coefficient of restitution between the plane and ball is e. The inclination of the plane is
45∘
tan−1e
tan−1√e
tan−1(e2)
The correct Answer is:C
To solve the problem, we need to analyze the motion of a ball dropped on a smooth inclined plane and how it behaves after the impact. The coefficient of restitution (e) plays a crucial role in determining the angle of inclination (θ) of the plane.
1. Understanding the Setup:
- Let the inclined plane make an angle θ with the horizontal.
- The ball is dropped vertically onto the inclined plane and moves horizontally after the impact.
2. Components of Velocity:
- When the ball is dropped, it has a vertical velocity component. Let’s denote this initial vertical velocity as u.
- The velocity components just before impact can be resolved into two directions: parallel and perpendicular to the inclined plane.
3. Velocity Components:
- The component of the velocity perpendicular to the inclined plane is ucosθ.
- The component of the velocity parallel to the inclined plane is usinθ.
4. Applying the Coefficient of Restitution:
- According to the definition of the coefficient of restitution, the velocity component after the impact perpendicular to the plane is given by:
Vsin(90−θ)=e⋅(ucosθ)
- Since sin(90−θ)=cosθ, we can rewrite this as:
Vcosθ=e⋅(ucosθ)
- From this, we can simplify to:
V=e⋅u
5. Parallel Component of Velocity:
- The velocity component parallel to the inclined plane remains unchanged:
Vsin(90−θ)=usinθ
- Again, substituting sin(90−θ)=cosθ:
Vsinθ=usinθ
- Thus, we have:
Vcosθ=usinθ
6. Setting Up the Equations:
- From the two equations derived:
1. V=e⋅u
2. Vcosθ=usinθ
7. Dividing the Equations:
- Dividing the second equation by the first:
VcosθV=usinθe⋅u
- This simplifies to:
cosθ=sinθe
8. Using Trigonometric Identities:
- Rearranging gives us:
e=sinθcosθ=tanθ
- Thus, we can express e in terms of tanθ.
9. Final Expression:
- Squaring both sides gives:
e=tan2θ
- Therefore, taking the square root:
tanθ=√e
- Finally, the angle of inclination is:
θ=tan−1(√e)
Final Answer:
The inclination of the plane is given by:
θ=tan−1(√e)
- Let the inclined plane make an angle θ with the horizontal.
- The ball is dropped vertically onto the inclined plane and moves horizontally after the impact.
- When the ball is dropped, it has a vertical velocity component. Let’s denote this initial vertical velocity as u.
- The velocity components just before impact can be resolved into two directions: parallel and perpendicular to the inclined plane.
- The component of the velocity perpendicular to the inclined plane is ucosθ.
- The component of the velocity parallel to the inclined plane is usinθ.
- According to the definition of the coefficient of restitution, the velocity component after the impact perpendicular to the plane is given by:
Vsin(90−θ)=e⋅(ucosθ)
- Since sin(90−θ)=cosθ, we can rewrite this as:
Vcosθ=e⋅(ucosθ)
- From this, we can simplify to:
V=e⋅u
- The velocity component parallel to the inclined plane remains unchanged:
Vsin(90−θ)=usinθ
- Again, substituting sin(90−θ)=cosθ:
Vsinθ=usinθ
- Thus, we have:
Vcosθ=usinθ
- From the two equations derived:
1. V=e⋅u
2. Vcosθ=usinθ
- Dividing the second equation by the first:
VcosθV=usinθe⋅u
- This simplifies to:
cosθ=sinθe
- Rearranging gives us:
e=sinθcosθ=tanθ
- Thus, we can express e in terms of tanθ.
- Squaring both sides gives:
e=tan2θ
- Therefore, taking the square root:
tanθ=√e
- Finally, the angle of inclination is:
θ=tan−1(√e)
The inclination of the plane is given by:
θ=tan−1(√e)
Similar Questions
A ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
View SolutionThe force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is .
View SolutionIn the situation shown, the force required to just move a body up an inclined plane is double the force required to just prevent the body from sliding down the plane. The coefficient of friction between the block and plane is μ. The angle of inclination of the plane from horizontal is given by :

View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionA ball is dropped on a large smooth inclined plane of angle of inclination 37∘, from a height of 209m above the point of impact. The coefficient of restitution of the impact is e=916 then :
[Take g=10m/s2]
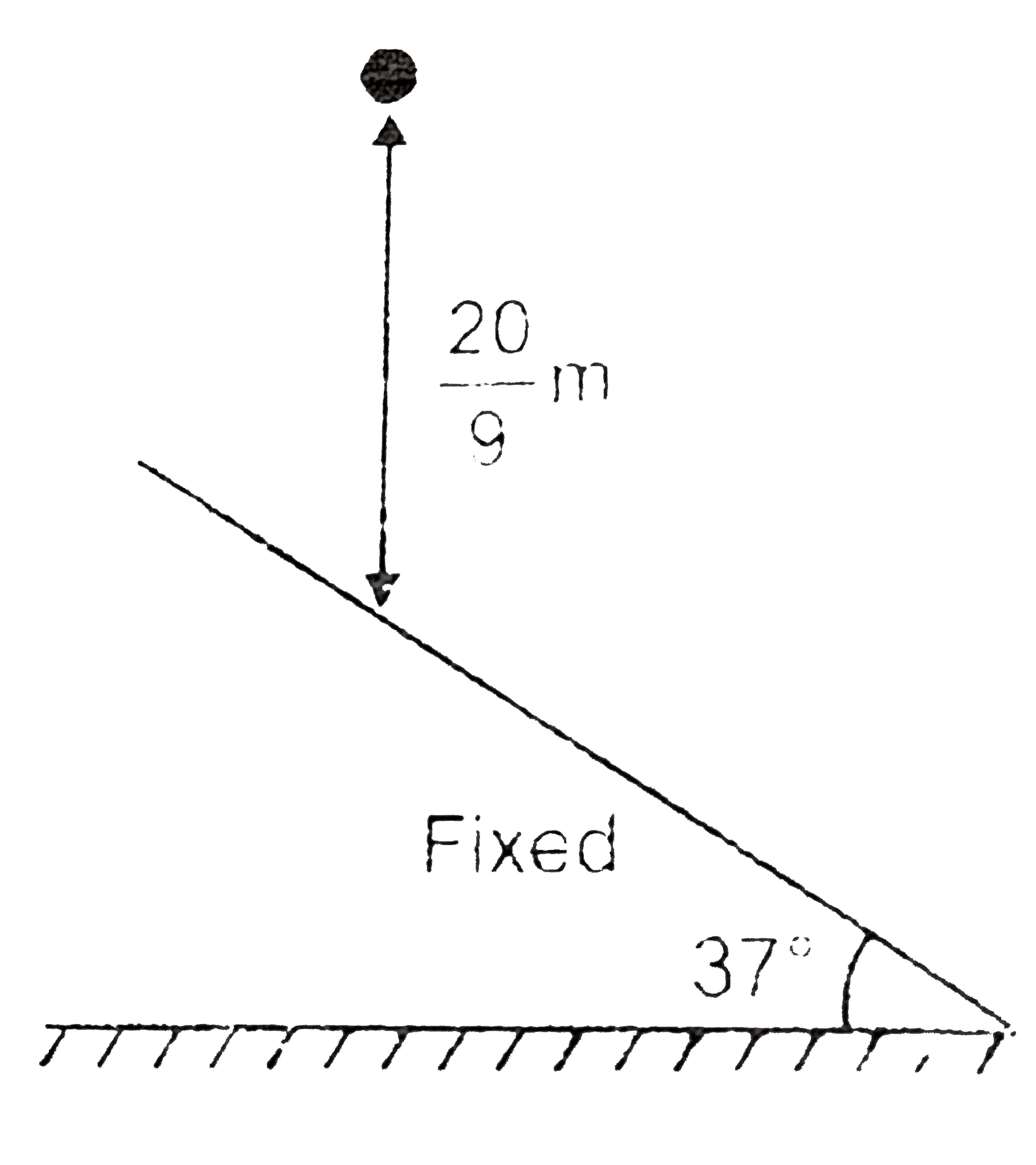
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient offriction between chain and inclined plane is μ, the maximum length of the lianging part to prevent the chain from falling vertically is:
View Solution
