If x2ay3b=e5m,x3cy4d=e2n,Δ1=∣∣∣5m3b2n4d∣∣∣,Δ2=∣∣∣2a5m3c2n∣∣∣andΔ3=∣∣∣2a3b3c4d∣∣∣, then the values of x and y are
Δ1Δ3,Δ2Δ3
Δ2Δ1,Δ3Δ1
log(Δ1Δ3),log(Δ2Δ3)
eΔ1Δ3,eΔ2Δ3
The correct Answer is:D
To solve the given problem step-by-step, we will use logarithmic properties and determinants. Let's break down the solution:
Step 1: Set Up the Equations
We start with the equations given in the problem:
1. x2ay3b=e5m
2. x3cy4d=e2n
Step 2: Take Logarithms
Taking the natural logarithm on both sides of each equation:
1. From x2ay3b=e5m:
2alnx+3blny=5m
2. From x3cy4d=e2n:
3clnx+4dlny=2n
Step 3: Write in Matrix Form
We can express these equations in matrix form:
(2a3b3c4d)(lnxlny)=(5m2n)
Step 4: Apply Cramer’s Rule
Using Cramer's rule, we can find lnx and lny:
1. For lnx:
lnx=Δ1Δ
where Δ1 is the determinant of the matrix formed by replacing the first column with the constants on the right side:
Δ1=∣∣∣5m3b2n4d∣∣∣=(5m)(4d)−(3b)(2n)=20md−6bn
And Δ is the determinant of the original coefficients:
Δ=∣∣∣2a3b3c4d∣∣∣=(2a)(4d)−(3b)(3c)=8ad−9bc
Thus,
lnx=20md−6bn8ad−9bc
2. For lny:
lny=Δ2Δ
where Δ2 is the determinant formed by replacing the second column:
Δ2=∣∣∣2a5m3c2n∣∣∣=(2a)(2n)−(5m)(3c)=4an−15mc
Thus,
lny=4an−15mc8ad−9bc
Step 5: Exponentiate to Find x and y
Now we can find x and y by exponentiating the logarithmic results:
1. x=elnx=e20md−6bn8ad−9bc
2. y=elny=e4an−15mc8ad−9bc
Final Answer
Thus, the values of x and y are:
x=e20md−6bn8ad−9bc,y=e4an−15mc8ad−9bc
We start with the equations given in the problem:
2. x3cy4d=e2n
Taking the natural logarithm on both sides of each equation:
2alnx+3blny=5m
3clnx+4dlny=2n
We can express these equations in matrix form:
Using Cramer's rule, we can find lnx and lny:
lnx=Δ1Δ
where Δ1 is the determinant of the matrix formed by replacing the first column with the constants on the right side:
Δ1=∣∣∣5m3b2n4d∣∣∣=(5m)(4d)−(3b)(2n)=20md−6bn
Δ=∣∣∣2a3b3c4d∣∣∣=(2a)(4d)−(3b)(3c)=8ad−9bc
lnx=20md−6bn8ad−9bc
lny=Δ2Δ
where Δ2 is the determinant formed by replacing the second column:
Δ2=∣∣∣2a5m3c2n∣∣∣=(2a)(2n)−(5m)(3c)=4an−15mc
lny=4an−15mc8ad−9bc
Now we can find x and y by exponentiating the logarithmic results:
2. y=elny=e4an−15mc8ad−9bc
Thus, the values of x and y are:
x=e20md−6bn8ad−9bc,y=e4an−15mc8ad−9bc
Similar Questions
If xayb=em,xcyd=en,Δ1=∣∣∣mbnd∣∣∣,andΔ2=∣∣∣amcn∣∣∣andΔ3=∣∣∣abcd∣∣∣, then the values of x and y are
View SolutionIf Δ1=∣∣ ∣ ∣∣2abe2def4x2y2z∣∣ ∣ ∣∣,Δ2=∣∣ ∣ ∣∣f2de2z4x2ye2ab∣∣ ∣ ∣∣, then the value of Δ1−Δ2 is
View SolutionIf 2(2n+5)=3 (3n−10), then n=
(a)5 (b) 3 (c)7 (d) 8
View SolutionGiven A=∣∣ ∣ ∣∣ab2cde2flm2n∣∣ ∣ ∣∣,B=∣∣ ∣ ∣∣f2de2n4l2mc2ab∣∣ ∣ ∣∣ , then the value of B/A is ___________.
View SolutionIf x3−2x2y2+5x+y−5=0 and y(1)=1, then (a)y′(1)=43 (b) y'(1)=−43 (c)y''(1)=−82227 (d) y′(1)=23
View SolutionThe solution of the differential equation x+x33!+x55!+1+x22!+x44!+=dx−dydx+dyis (a) (b)(c)2y(d)e(e)(f)2x(g)(h)=C(i)e(j)(k)2x(l)(m)+1(n) (o) (p) (q)(r)2y(s)e(t)(u)2x(v)(w)=C(x)e(y)(z)2x(aa)(bb)−1(cc) (dd) (ee) (ff)(gg)y(hh)e(ii)(jj)2x(kk)(ll)=C(mm)e(nn)(∞)2x(pp)(qq)+2(rr) (ss) (d) None of these
View SolutionIf ΔABC~ΔDEF such that BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)=
View SolutionLet A and B be two sets such that n(A)=5 and n(B)=2, if a, b, c, d, e are distinct and (a,2), (b,3), (c,2), (d,3), (e,2) are in A×B , find A and B.
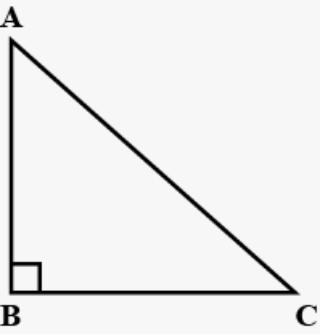
View SolutionIn the given figure, ΔABC,AB=3cm,BC=4cm and AC=5cm. Name the smallest and the largest angles of the triangle.
View SolutionIf (x,3)and (3,5) are the extremities of a diameter of a circle with centre at (2,y) then the values of x and y are a. (3,1) b. x=4,y=1 c. x=8,y=2 d. none of these
View Solution
